今回は、3次元の空間の中を視点が動くプログラムを作ってみます。
上の画面が今回の最終形です。
視点をスライドパッドで前後左右に移動し、十字キー上下で上下に移動し、L・Rボタンで左右に回転します。
物体のほうは水平面上に格子状に等間隔に並べてあり、位置は固定です。
前回は、スクリーンは3次元の立方体の空間の1つの面に固定されていました。
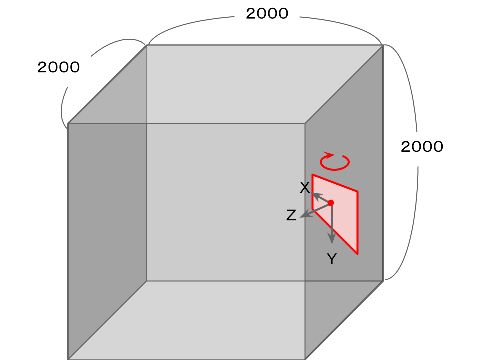
今回はスクリーンが下図のように空間の中を移動します。
ただし、視点から見た画像をスクリーン上に構成するためには、最終的にはすべての物体の座標を「スクリーンの中央を原点とした座標系」の上で表現する必要があります。
これは、スクリーンがある方向に移動したということを、空間全体を反対方向に移動させて表現するということになります。
つまり「プチコン3号 4日目 背景をスクロールさせる」と同じです。
さらにこれに加えて、視点の回転を表現するために、座標をY軸周りに回転することが必要です。
回転による座標の変換は、三角関数を使います。
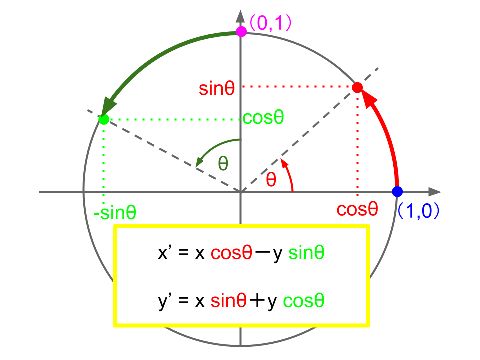
円周の上にある点が、円周上を角度θだけ回転するとき、
・座標(x,0)は(x cosθ, x sinθ)に
・座標(0,y)は(-y sinθ, y cosθ)に
それぞれ移ります。
座標(x, y)を角度θだけ回転すると、上の2つを重ね合わせた
(x cosθ-y sinθ, x sinθ+y cosθ)
へ移ります。
以上を使って、まず「2次元平面の上をスプライトが方向転換しながら移動するプログラム」を作ってみました。
ちょうど、3次元の立方体の空間を真上から見ているようなイメージです。
座標系で言うと、XZ平面を表示していることになります。
といっても、実際には普通の2次元のプログラムです。
ただし操作がちょっと変わっています。
△のスプライトを画面内で動かすのですが、動きは「回転+前後左右への移動」で表現します。
L,Rのボタンは、その場でスプライトが左回り・右回りに回転します。
スライドパッドは、上方向が「前」、下方向が「後」への移動です。
つまり、スライドパッドを上に動かすと、そのときスプライトが向いている方向に進むわけです。
スライドパッドの左右は、そのときスプライトが向いている方向に対して、左右へ(向きを変えずに)移動します。
DEF ROTATE X,Y,T OUT X1,Y1 X1=COS(T)*X - SIN(T)*Y Y1=SIN(T)*X + COS(T)*Y END ACLS DIM X[100],Z[100] FOR I=0 TO 99 X[I] = -90 + 20*(I MOD 10) Z[I] = -90 + 20*FLOOR(I / 10) NEXT FOR I=0 TO 99 GPSET X[I]+200,-Z[I]+120 NEXT SPSET 0,2353 T=0:U=0:W=0 @LOOP B=BUTTON(0) IF B AND 256 THEN T=T-0.1 IF B AND 512 THEN T=T+0.1 SPROT 0,DEG(T) STICK OUT DX,DY ROTATE DX,DY,-T OUT DX,DY U=U + DX*5 W=W + DY*5 SPOFS 0,U+200,-W+120 VSYNC 1 GOTO @LOOP
手続きROTATE X,Y,Tは、座標(X,Y)を角度Tだけ回転し、その結果をX1,Y1へ返します。
中で使っている数式は、先ほど説明したとおりのものです。
点を100個用意し、(-90,-90)から(90,90)の範囲に10×10の格子状に並べています。
点の座標は、配列XとZに格納しています。
表示はグラフィック画面上に1度だけ行っています。
なお、座標はXZ平面ですので、原点がスクリーン中央、X軸は左から右、Z軸は下から上に向かいます。
ループの中で、スライドパッドとL・Rボタンでスプライトを操作しています。
スプライトのXZ平面上での座標は、(U, W)で、向き(回転角)がT(単位はラジアン)です。
3次元空間でのY軸は、画面の手前から奥に向かう方向になります。
このとき、Y軸周りの回転の角度は、画面上では時計回りが正となります。
従って、Lボタンを押したときはTを減らし、Rボタンを押したときTを増やしています。
そして、SPROTでスプライトを回転させます。
SPROTの角度指定はラジアンではなく度(DEGREE)なので、関数DEGで変換します。
なおSPROTの角度指定は、時計回りが正です。
スライドパッドから読み取った移動量も、スプライトの向きに合わせて回転させます。
この計算は最初に定義した関数ROTATEを使いますが、この関数では角度指定が反時計回りが正です。
そのため、回転角はTではなく-Tを指定しています。
さて、実際に上のプログラムを動作させてみると、実に操作しづらいです。
スライドパッドを動かす方向と、スプライトが動く方向とが一致しないのだから当たり前です。
このプログラムを、スプライトは位置も向きも固定して、格子点のほうを移動させたり回転させたりするように変更したのが、次のプログラムです。
DEF ROTATE X,Y,T OUT X1,Y1 X1=COS(T)*X - SIN(T)*Y Y1=SIN(T)*X + COS(T)*Y END ACLS DIM X[100],Z[100] FOR I=0 TO 99 X[I] = -90 + 20*(I MOD 10) Z[I] = -90 + 20*FLOOR(I / 10) NEXT SPSET 0,2353 SPOFS 0,200,120 T=0:U=0:W=0 @LOOP B=BUTTON(0) IF B AND 256 THEN T=T-0.1 IF B AND 512 THEN T=T+0.1 STICK OUT DX,DY ROTATE DX,DY,-T OUT DX,DY U=U + DX*5 W=W + DY*5 GCLS FOR I=0 TO 99 ROTATE X[I]-U,Z[I]-W,T OUT X1,Z1 GPSET X1+200,-Z1+120 NEXT VSYNC 1 GOTO @LOOP
格子点の描画をループの内側に移動し、座標はスプライトの位置(U,W)の周りに角度Tだけ回転しています。
回転方向は、スプライトを回転させる場合と逆方向にする必要がありますが、もともとTは時計回りが正であるのに対してROTATEは反時計回りが正ですので、Tをそのまま渡せば逆方向の回転になっています。
さて、以上で準備ができました。
次にこの100個の格子点の座標を、前回のようにZの値に応じて縮小し、遠近感を出してみましょう。
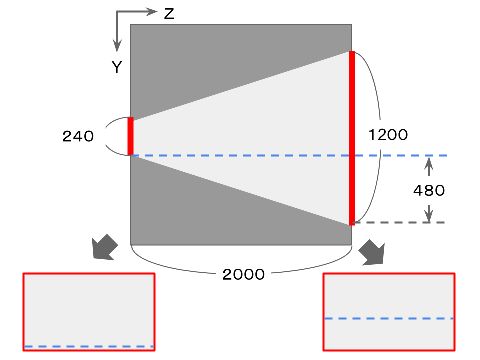
前回はX座標の縮小を図示しましたので、今回はY座標の縮小を図示してみました。
回転のことを考えなければ、スクリーンはZ=0の平面上にあり、縦方向のサイズは240ピクセルです。
Z=2000のとき、高さ1200ピクセル分がスクリーンの240ピクセルの中に納まることになります。
原点はスクリーン中央、Y軸は下向きが正です。
格子点は、青い点線のところにあるとしましょう。
これはY=120のXZ平面です。
Z=0のとき、この平面はスクリーンの最下部に表示されます。
Z=2000のときは、Y = -600~+600 の範囲がスクリーンに表示されますので、Y=120の平面はスクリーン上では1/5に縮小され、Y=25となります。
当然のことながら、この縮小率はX座標の縮小率と同じ値ですので、Y座標のための特別な計算は不要です。
では、格子点の座標の縮小を行ったプログラムです。
このプログラムで、視点の移動や回転の処理は完成です。
DEF ROTATE X,Y,T OUT X1,Y1 X1=COS(T)*X - SIN(T)*Y Y1=SIN(T)*X + COS(T)*Y END ACLS DIM X[100],Z[100] FOR I=0 TO 99 X[I] = -450 + 100*(I MOD 10) Z[I] = -450 + 100*FLOOR(I / 10) NEXT T=0:U=0:V=0:W=0 @LOOP B=BUTTON(0) IF B AND 256 THEN T=T-0.01 IF B AND 512 THEN T=T+0.01 IF B AND 1 THEN V=V-10 IF B AND 2 THEN V=V+10 STICK OUT DX,DY ROTATE DX,DY,-T OUT DX,DY U=U + DX*5 W=W + DY*5 GCLS FOR I=0 TO 99 ROTATE X[I]-U,Z[I]-W,T OUT X1,Z1 SCALE=400/(400+1600*(Z1/2000)) GPSET X1*SCALE+200,(-V+120)*SCALE+120 NEXT VSYNC 1 GOTO @LOOP
赤い箇所が変更点です。
前回同様の座標変換処理と、Y軸方向への移動処理を追加しています。
格子点の間隔が、元のプログラムのままでは狭すぎるので、(-450,-450)から(450,450)の範囲に並ぶように変更しています。
視点=スクリーンの中央の点の3次元空間内での位置は、座標(U,V,W)で表されます。
スライドパッドと、上下ボタンでこの座標を移動させています。
前回の記事と同様に縮小率の計算を行い、格子点のX座標とY座標を縮小しています。
縮小前のY座標は、さきほど説明したとおり、Y=120で一定ですが、描画時の座標は視点からの相対座標になりますので、-V+120になります。
それでは、最後に格子点の場所にスプライトを置いて、本格的に擬似3Dにしてみましょう。
スプライトはそのままでは16×16ピクセルと小さいので、12倍に拡大し、Z=0のときに192×192ピクセルになるようにしてみました。
これがこの記事の冒頭の画面を生成したプログラムです。
お花畑の中を散歩してみてください。
DEF ROTATE X,Y,T OUT X1,Y1 X1=COS(T)*X - SIN(T)*Y Y1=SIN(T)*X + COS(T)*Y END ACLS DIM X[100],Z[100] FOR I=0 TO 99 X[I] = -1800 + 400*(I MOD 10) Z[I] = -1800 + 400*FLOOR(I / 10) SPSET I,2067 NEXT T=0:U=0:V=0:W=0 @LOOP B=BUTTON(0) IF B AND 256 THEN T=T-0.01 IF B AND 512 THEN T=T+0.01 IF B AND 1 THEN V=V-10 IF B AND 2 THEN V=V+10 STICK OUT DX,DY ROTATE DX,DY,-T OUT DX,DY U=U + DX*10 W=W + DY*10 FOR I=0 TO 99 ROTATE X[I]-U,Z[I]-W,T OUT X1,Z1 SCALE=400/(400+1600*(Z1/2000)) IF Z1<-256 THEN SPHIDE I:CONTINUE SPSHOW I Z1=Z1/4 IF Z1>1024 THEN Z1=1024 C=127+128*SCALE SPCOLOR I,RGB(255,C,C,C) SPSCALE I,12*SCALE,12*SCALE SPOFS I,X1*SCALE+200,(-V+120)*SCALE+120,Z1 NEXT VSYNC 1 GOTO @LOOP
スプライトが192ピクセルだと、格子点の間隔が200ピクセルでは狭すぎますので、400ピクセル間隔にして(-1800,-1800)から(1800,1800)の範囲に配置しました。
この格子点の1つ1つに、スプライトを1つ置きます。
また、これによってフィールドが広くなったので、視点の移動速度を2倍にしています。
スプライトは、SPOFSでZ座標を指定できますが、値は(-256~1024)でなければなりません。
Zが-256より小さいものは、視点よりも後方にあるスプライトなので、SPHIDEで表示を抑制しています。
一方、Z値が1024より大きい場合ですが、全て上限値1024にしてしまうと、遠くにあるスプライトが沢山重なってしまい、違和感があります。
このため、SPOFSで指定するZ値は実際のZ値の1/4にしています。
格子点のエリア全体が3600×3600ですので、1/4にすれば全体を表示してもZ値は1024以下に収まります。
このほか、前回同様、遠くにあるスプライトほど色を暗くしています。







コメント