前回作成したウエーブテーブルシンセサイザは、起動時にウエーブテーブルを計算で生成していました。しかし一般的には、ウエーブテーブルは事前に生成して定数としてコードに埋め込むのが普通でしょう。
例えばPythonなどを使ってウエーブテーブルを生成し、事前に音を確認した上で、その波形をCの配列として出力させてソースコードに取り込むといった手順が考えられます。
今回は、前回と同じサイン波のウエーブテーブルを、PythonでCのヘッダファイルとして生成してみます。
サイン波のウエーブテーブルを生成するPythonのコードは以下のようになります。
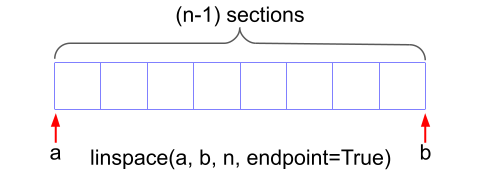
numpyのlinespace(a, b, n)は区間[a, b]をn-1個に分割したリストを出力します。
リストの先頭の値はa、末尾の値はbで長さはnです。末尾の値を含めたくない場合は、endpoint=Falseを指定します(デフォルトはTrue)。
前回の記事で説明したように、ウエーブテーブルの末尾には補間処理のために1つ余分にデータを付け加えたいので、今回はnをテーブルサイズ+1にしています。
zerosは値がゼロで埋まったリストを生成します。データ型はデフォルトはfloat64ですが、float32を使いたいのでdtypeで指定しています。
10行目以降は結果を出力するためのコードです。
これを実行すると次のようなヘッダファイルが出力されます。
#define w_tbl_size 128
float w_tbl[w_tbl_size + 1] =
{
0.0, 0.024541229, 0.049067676, 0.07356457, 0.09801714, 0.12241068, 0.14673047, 0.17096189, 0.19509032,
0.21910124, 0.24298018, 0.26671275, 0.29028466, 0.31368175, 0.33688986, 0.35989505, 0.38268343,
0.4052413, 0.42755508, 0.44961134, 0.47139674, 0.4928982, 0.51410276, 0.53499764, 0.55557024,
0.57580817, 0.5956993, 0.6152316, 0.6343933, 0.65317285, 0.671559, 0.68954057, 0.70710677,
0.7242471, 0.7409511, 0.7572088, 0.77301043, 0.7883464, 0.8032075, 0.8175848, 0.8314696,
0.8448536, 0.8577286, 0.87008697, 0.8819213, 0.8932243, 0.9039893, 0.9142098, 0.9238795,
0.9329928, 0.94154406, 0.94952816, 0.95694035, 0.96377605, 0.97003126, 0.9757021, 0.98078525,
0.98527765, 0.9891765, 0.99247956, 0.9951847, 0.99729043, 0.99879545, 0.9996988, 1.0,
0.9996988, 0.99879545, 0.99729043, 0.9951847, 0.99247956, 0.9891765, 0.98527765, 0.98078525,
0.9757021, 0.97003126, 0.96377605, 0.95694035, 0.94952816, 0.94154406, 0.9329928, 0.9238795,
0.9142098, 0.9039893, 0.8932243, 0.8819213, 0.87008697, 0.8577286, 0.8448536, 0.8314696,
0.8175848, 0.8032075, 0.7883464, 0.77301043, 0.7572088, 0.7409511, 0.7242471, 0.70710677,
0.68954057, 0.671559, 0.65317285, 0.6343933, 0.6152316, 0.5956993, 0.57580817, 0.55557024,
0.53499764, 0.51410276, 0.4928982, 0.47139674, 0.44961134, 0.42755508, 0.4052413, 0.38268343,
0.35989505, 0.33688986, 0.31368175, 0.29028466, 0.26671275, 0.24298018, 0.21910124, 0.19509032,
0.17096189, 0.14673047, 0.12241068, 0.09801714, 0.07356457, 0.049067676, 0.024541229, 1.2246469e-16,
};
上のPythonスクリプトの末尾に以下のようなコードを追加すると、生成した波形を画面上で確認できます。
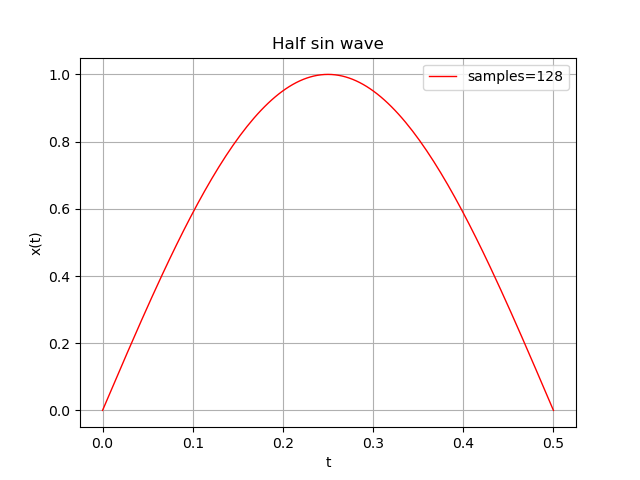
なお、ウエーブテーブルを元に、wavファイルを生成したければ、下記のリンク先の記事が参考になります。

さて、よく知られているように、浮動小数点数はコンピュータ内部では一種の「分数」として表現されており、上のように小数でプリントアウトしても、内部の値と完全には一致しません。
つまり、上のようにプリントアウトする時点で誤差が生じ、プリントアウトした結果を読み込む際にも誤差が生じます。一般論としては、浮動小数点数の演算では常に誤差を意識する必要があります。
浮動小数点数の内部表現をそのままやり取りできれば、誤差なく数値を入出力することができます。
ただ、そのための標準的なフォーマットは現在存在していないようです。floatの内部表現そのものは共通ですが、エンディアンの違いは考慮されませんので、バイト列をやり取りする場合は注意が必要です。下記のリンク先の図が分かりやすいです。
トリッキーですが、float型の内部表現である32bitの値を、32bit符合無し整数としてプリントアウトし、それを読み込んだ後でfloat型に戻せば、誤差なく数値を渡すことができます。エンディアンの違いは符合無し整数を読み書きする際に補正されるからです。
例えばfloat型の「2.0」はunsigned intの「0x40000000」と同じビットパターンであり、float型の「0.15625」はunsigned intの「0x3e200000」と同じビットパターンです。
float型を32bit符合無し整数にするPythonのコードは以下のようになります。
import struct
def float_to_uint32(f):
bin = struct.pack('f', f)
i = struct.unpack('I', bin)[0]
return hex(i)
これを受け取るC言語側のコードですが、
・uint32_t型の配列として受け取り、その配列をfloat *型へタイプキャストする
・uint32_tとfloatのunion型の配列として受け取り、その配列の要素をfloat型としてアクセスする
といった方法が考えられます。
前者は以下のような感じになります。
uint32_t wavetable_i[wavetbl_size + 1] =
{
0x0, 0x3cc90ab0, ...
float *wavetable_f = (float *) wavetable_i;
後者はこんな感じです。なお、共用体で初期値の代入に使えるのは先頭の型(上の場合、uint32_t)だけです。
union uint_float {
const uint32_t t_uint;
const float t_float;
};
union uint_float wavetable_u[wavetbl_size + 1] =
{
0x0, 0x3cc90ab0, ...
__fast_inline float wavetable_f(int i) {
return wavetable_u[i].t_float;
}
今回は、uint32_tでアクセスするのは初期化のときだけで、利用はfloatのみなので、分かりやすいのは前者のほうでしょうか。

コメント