前回、ワイヤーフレームで3D空間を表現しましたが、今回からは11日目で作成した迷路探検ゲームの3D版を作ってみます。
プチコン3号 11日目 当たり判定を追加して迷路探検ゲーム完成!: 楽しくやろう。
前回のプログラムでは、線画で碁盤目状の地面を表示しました。
迷路の3Dでの表示は、この碁盤目に沿って垂直に壁を立てれば実現できます。
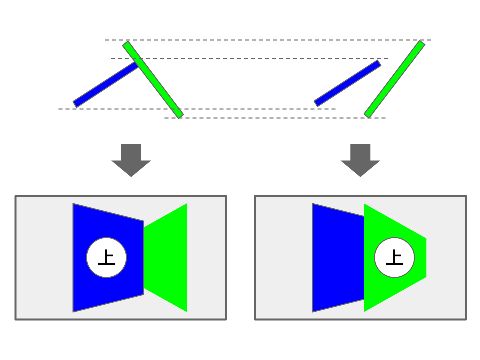
具体的には、まず迷路を二次元で作ってから、前回同様に視点からの距離に応じて縮小してやると、地面に迷路を描くことができます。(下図の青のライン)
次に、画面の下半分を鏡に映すように画面上半分に反転して表示します。(下図の緑のライン)
最後に、下半分と上半分の対応する点同士を垂直線で結んでやれば出来上がりです。(下図の赤のライン)
もちろんこれだけでは不十分で、壁の向こう側が見えないように、迷路の壁は塗りつぶさなければなりません。
これには、プチコン3号の3.1.0へのバージョンアップで追加された、塗りつぶした三角形の描画命令GTRIが使えます。
ただしGTRI命令で描けるのは、二次元の三角形です。
三次元ポリゴンの描画では、ポリゴン同士の重なり具合が座標のZ値を正しく反映していなければなりません。
具体的には、ポリゴンが重なる時は、Z値が小さいもの(視点により近いもの)が上になる必要があります。
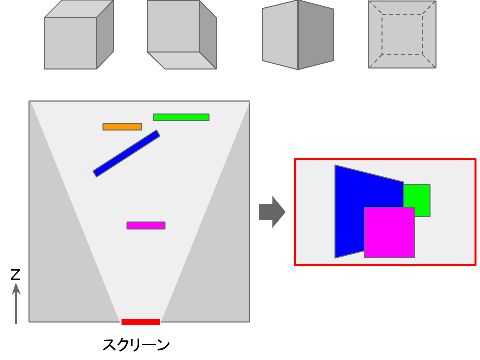
例えば立方体を描く場合、下図のように色々な見え方があります。
どの見え方になるかは、立方体の各面と視点との位置関係に依存しています。
視点の移動や回転によってZ値は変化しますので、重なる順序も時々刻々変化します。
上の図の下半分は、左側がいろいろな壁が立っている様子を上空から眺めた図で、スクリーンは赤い位置にあります。
右側が、スクリーンからの見え方です。
手前の壁が後の壁を隠しています。
このように、重なりなどの影響を考慮して、見えている部分だけを画面に描画する処理を「隠面消去」といいます。
陰面消去には様々な方法がありますが、遠方のものから順に描画する「Zソート法」もその一つです。
この方法では、全てのポリゴンをZ軸の値の大きさで並べ替えてから、Z値が大きい順に描画します。
上の図で言えば、
緑→オレンジ→青→ピンク
の順にポリゴンを描けば、右のような画像が得られます。
ただ、この方法は面同士が交差する場合は利用できません。
一方、三次元グラフィックスのハードウェアで広く用いられているのが「Zバッファ法」です。
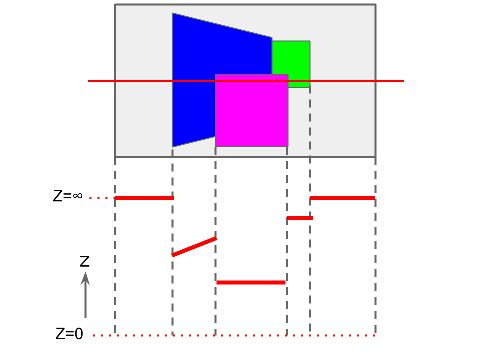
これは、スクリーンの各ピクセルについて、描画時のZ値をバッファに保持しておくものです。
新しい3次元のピクセルを描画する際に、Zバッファの対応する値と、描こうとするピクセルのZ値を比較します。
そして、Zバッファの値のほうが大きければ、スクリーンを新しいピクセルで、ZバッファをそのピクセルのZ値で、それぞれ上書きします。
例えば、下図の画面中央の赤いラインに対応するZバッファは、図の下のような値を取ります。
前置きが長くなりましたが、上で述べたのは(擬似でない)三次元グラフィックスの一般論です。
迷路を三次元で描くことに限定すると、一般論よりも手抜きができます。
迷路の壁のポリゴンには、以下のような非常に強い制約条件があるからです。
・XZ平面に対して垂直である
・全ての壁で、幅や高さが同一である
・規則正しく配置されており、交差はしない
これらの制約条件を前提にすると、
「全ての壁の重なり具合は
・ある特定のY(ただし0<Y<壁の高さ)の場合について
・各壁のZ値の最大値(あるいは最小値、平均値など1つの値)を調べれば十分」
であることが分かります。
壁が垂直、かつ全ての壁の高さが同じなので、Yの値が変わっても重なり具合は変わりません。
壁が碁盤目状に配置されているので、2つの壁のどちらが手前にあるかも代表点の座標比較だけで決まります。
ちなみに碁盤目状でない場合は、垂直な壁であっても、Z値だけではどちらの壁が手前か判定できません。
下図の2つのパターンは、どちらも各壁のZ値の最大値、最小値は同じですが、壁の重なり方は異なっています。
今回は、以下のようなアルゴリズムで隠面消去を行っています。
(1)全ての壁を、高さ1ピクセル横400ピクセルのZバッファに描画する
(ただしZ値はまじめに計算せず、壁の2つの端点の平均値を採用)
(1’)描画時に、各ピクセルが表示している壁の番号を、長さ400の配列に記録する
(2)壁の番号の配列を、Z値が大きい順に並べ替える
(3)壁の番号の配列の順に壁を描く
このアルゴリズムは、表示すべきポリゴンの抽出を(1)でZバッファ法で行い、抽出したポリゴンの描画は(2)でZソート法で行っていることになります。
今回のアルゴリズムは、隠れている壁を描画しなくて済むので、描画処理を大幅に短縮できます。
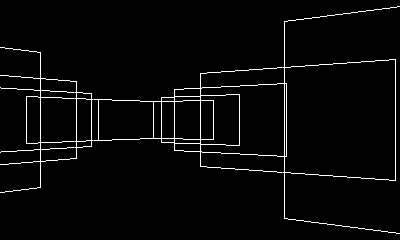
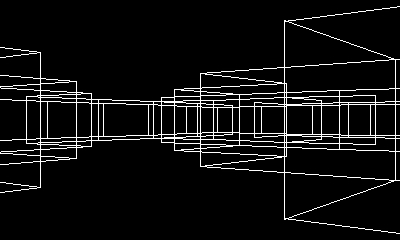
このような処理をせずに、迷路の壁を普通に全てワイヤーフレームで描くと、例えば以下のようになります。
これをすべて遠い順にGTRI命令で描画すると、さすがにアニメーションさせるのは困難です。
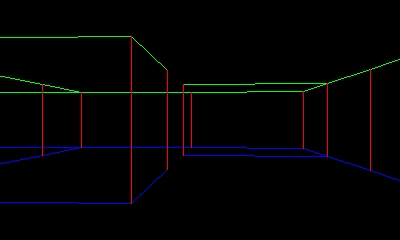
上記のアルゴリズムを使って、「見える壁」だけを抽出すると、以下のようになります。
この場合は、壁の枚数は10枚ですので、GTRI命令20回で描画することができます。
この程度の回数であれば、プチコン3号でも、何とかアニメーションができる程度の時間で描画できます。
遠くの壁から順に描画すると、以下のような画像ができます。
プログラムですが、全体はMiiverseにアップロードしてあります。
公開キーは【4R2EP4K3】です。
サイズが大きいので、今回は上記の隠面処理の部分だけを抜き出して掲載します。
FOR I=0 TO 399 ZBUF[I]=POW(2,31) W_VISIBLE[I]=-9999 NEXT FOR I=0 TO LEN(W_BGN)-1 P1=W_BGN[I] P2=W_END[I] L[0]=R_X[P1]:L[1]=R_Z[P1] L[2]=R_X[P2]:L[3]=R_Z[P2] IF !CLIPLINE(L,X_MIN,Z_MIN,X_MAX,Z_MAX) THEN CONTINUE X1=FLOOR(L[0]*SCALE_Z(L[1])+200) X2=FLOOR(L[2]*SCALE_Z(L[3])+200) IF X1>X2 THEN SWAP X1,X2 X1=MAX(X1,0) X2=MIN(X2,399) ZVAL=(R_Z[P1]+R_Z[P2])/2 FOR J=X1 TO X2 IF ZBUF[J]>ZVAL THEN ZBUF[J]=ZVAL W_VISIBLE[J]=I ENDIF NEXT NEXT
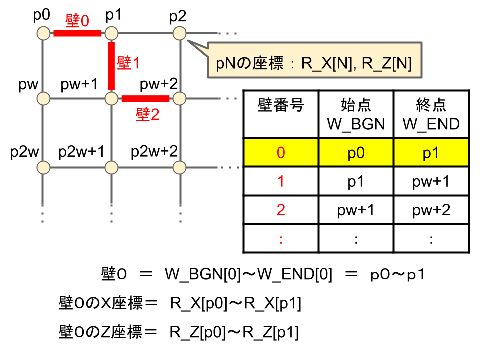
リストで使われている変数の意味は上の図を参照してください。
壁は始点と終点で表します。始点と終点は、図の左にあるように、格子の交差点につけた番号です。
図では、0番の壁の始点・終点はp0とp1です。1番の壁の始点・終点はp1とp(w+1)です。
壁の始点と終点は図右の表のように、始点が配列W_BGN、終点が配列W_ENDに格納されています。
点pの座標は、配列R_XとR_Zに格納されています。
最初のFOR…NEXTループは、2つの配列を初期化しています。
配列ZBUFはZバッファで、視点からの距離(Z値)を格納します。
Zバッファの各要素の初期値は無限大…としたいところですが、実際は十分大きな値(2の31乗=約20億)にしています。
W_VISIBLE[I]は、ZBUF[I]に表示される壁の番号が入ります。
初期値-9999は、「壁が表示されていない」ことを示すために使います。
次のFOR…NEXTループで、I番目の壁の処理を行います。
壁の端点のXZ座標は(R_X[P1], R_Z[P1])と(R_X[P2], R_Z[P2])です。
これを配列Lに設定し、Z>0の空間でクリッピングします。
これによって、視点よりも後方の壁は消去されます。
(クリッピングについては前回の記事を参照してください。)
表示される部分が無ければ、次の壁の処理に移ります。
表示される部分があった場合は、配列Lにクリッピング処理後の座標が入っています。
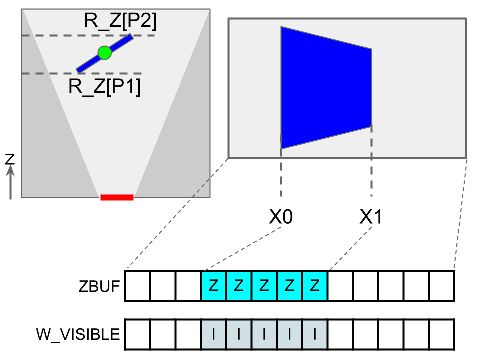
L[1]とL[3]がZ値で、これを元に縮小率を求め、画面上で壁が表示される範囲のX座標X0とX1を求めます。
そして、ZBUF[X0]..ZBUF[X1]にこの壁のZ値を代入します。
ただし、元からZBUFに入っていた値のほうがZ値よりも小さい場合には何もしません。
Z値は実際にはL[1]~L[3]まで変化しますが、先に書いたように壁が規則正しく並んでいるので、壁の中点(下図左上の緑色の点)のZ座標で代用します。
また、W_VISIBLE[X0]..W_VISIBLE[X1]には、この壁の番号Iを代入します。
次に、壁の描画処理です。
まず、作成したZバッファの値の大きい順に、W_VISIBLEをソート(並べ替え)します。
プチコン3号は、このための命令RSORTがあります。
RSORTは第一引数の配列を降順でソートしますが、第二引数以降の配列が与えられた場合は、それらの配列も同じ順序でソートします。
ソートした結果のW_VISIBLEは、表示されるピクセル数の分だけ、壁の番号が連続して並んでいます。
描画処理ではW_VISIBLEの先頭から順に、指定された番号の壁を描画していきます。
直前と同じ番号の壁はもう描画する必要が無いので、飛ばします。
緑色の部分が壁を1つ描くためのコードです。
壁は台形になるので、GTRI命令を2回使います。
また、壁の輪郭の縦線の部分をGLINEで描いています。
GCLS RSORT ZBUF,W_VISIBLE W_LAST=-9999 FOR I=0 TO LEN(W_VISIBLE)-1 IF W_VISIBLE[I]==W_LAST THEN CONTINUE W_LAST=W_VISIBLE[I] IF W_LAST==-9999 THEN CONTINUE P1=W_BGN[W_LAST] P2=W_END[W_LAST] L[0]=R_X[P1]:L[1]=R_Z[P1] L[2]=R_X[P2]:L[3]=R_Z[P2] IF CLIPLINE(L,X_MIN,Z_MIN,X_MAX,Z_MAX) THEN S1=SCALE_Z(L[1]) L[0]=L[0]*S1+200 L[1]=V*S1+120 S2=SCALE_Z(L[3]) L[2]=L[2]*S2+200 L[3]=V*S2+120 C=(S1+S2)/2*128+8 C=RGB(C,C,C) GTRI L[0],L[1],L[2],L[3],L[2],-L[3]+240,C GTRI L[0],L[1],L[0],-L[1]+240,L[2],-L[3]+240,C C=MAX(S1,S2)*128+32 C=RGB(C,C,C) GLINE L[0],L[1],L[0],-L[1]+240,C GLINE L[2],L[3],L[2],-L[3]+240,C ENDIF NEXT
以上で迷路の3D表示は終わりです。
次回は、3D迷路の中に敵を追加してみたいと思います。




コメント