前回、前々回とスプライトを使った擬似3D表示のプログラムを作ってきました。
しかし2Dのゲームと比べると背景が簡素になってしまいます。
2DではBGやスプライトを使用することができますが、どちらも回転と拡大しか行えません。
擬似3D表示では近くのものは大きく、遠くのものは小さく表示します。
これをBGやスプライトで実現するには台形型の変換(射影変換、ホモグラフィと呼ばれます)が必要ですが、プチコン3号ではこの変換はサポートされていません。
今回は、比較的高速に表示できる方法として、ワイヤーフレームの背景をGLINE命令で描いてみます。
前々回のプログラムで、GPSET命令で点を描画させましたので、座標変換は既にできています。
基本的には、この点と点を結べばワイヤーフレームの描画ができます。
ただし、線分を描画する場合には、点の描画には無かった問題が起こります。
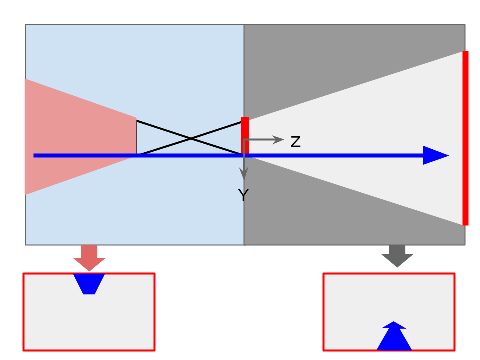
下図は、3次元の空間を横から見た状態(YZ平面)です。
中央近くの赤い縦線のところがスクリーンで、右方向がスクリーンから見た奥行き方向になります。
左方向はスクリーンよりも手前なので、表示させない領域です。
今、青い矢印のように線を描いたとします。
足元から、前方遠くに向かってまっすぐ線が延びているようなイメージです。
スクリーン上では、この線はスクリーンの下半分に「下から上に」伸びるように見えています。
この線がスクリーンよりも手前方向にも伸びていて、図左の赤い領域まで入っているとします。
すると、この線はスクリーン上では、スクリーンの上半分で「上から下に」延びているように見えます。
図の中央でスクリーン下端から延びる線とスクリーン上端から延びる線が交差していますが、この点より左側では縮小率が負になるため、上下が逆になってスクリーンへ投影されるのです。
この不要な表示を抑制するためには、「クリッピング」と呼ばれる処理が必要です。
点やスプライトを描画する場合には、Zが負の場合は単に描画しなければ済みました。
しかし、線や面のように広がりを持つものを描画する場合は、描画可能な部分だけを「切り取る」ことが必要です。
上の図で言えば、青い線分のうち、スクリーンよりも右側(Z>0)の領域を抽出することになります。
さらに、Z>0であっても、擬似3DのプログラムではGLINE命令に与えるXやYがスクリーンのサイズよりはるかに大きくなる場合があります。
ところがプチコン3号のGLINE命令は、現状(v3.1.0)ではやや不安定で、与えた座標値によってはプチコン3号自体がクラッシュすることがあります。
boochowp / boochowp
実行するとプチコン3号(3.1.0)が落ちます。GBOXやGFILLでは死なないので、GLINEのバグみたい。
GLINE 11,0,-110000,-11000 #petitcom at 03/06 16:22
GCLIP命令で描画範囲を制約することができますが、この命令を使っても使わなくても不安定さには変わりありませんでした。
そのため、スクリーンに描画する前にもスクリーンサイズでのクリッピングが必須です。
クリッピングについては、既に様々なアルゴリズムが考案されています。
「線分を矩形でクリッピングする」アルゴリズムとしては、Cohen-Sutherlandのアルゴリズムや、Liang-Barskyのアルゴリズムが知られています。
今回は、後者のLiang-Barskyのアルゴリズムでクリッピングを実装しました。
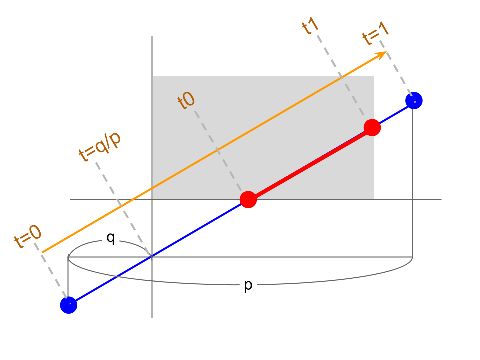
このアルゴリズムは、下図のように線分をtというパラメータで表現します。
t=0が線分の一方の端点を表し、t=1が線分のもう一方の端点を表します。
クリッピングされた線分はt0とt1という2つのパラメータで表されます。
このパラメータの求め方は以下のようになります。
まず、線分全体の長さのX値をp、線分の端点と矩形領域の左端との差分のX値をqとします。
すると、線分が矩形領域の左端と交差する点のt=q/pが求まります。
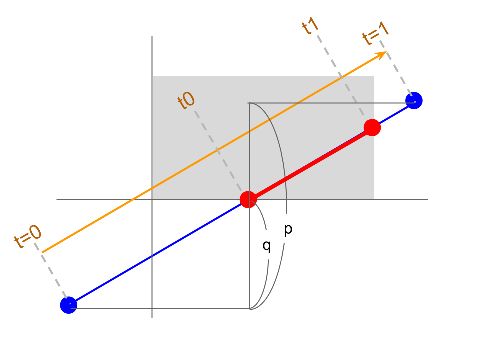
次に、下図のように、同じことをY座標についても行います。
すると同様に、線分が矩形領域の下端と交差する点のt=q/pが求まります。
この2つのtのうち、より値が大きいほうをt0として採用します。
t1についても同様の処理を行います。
2つのt1のうち、より小さい値をt1として採用します。
アルゴリズムの基本的な部分は以上で、このほか、線分が水平または垂直であった場合や、線分が交差しない場合などの処理が必要になります。
以下のページにこのアルゴリズムの図解やソースコードがあります。
(ただし、ソースコードはp==0の判定より前にq/pを求めているというバグがあります。)
Skytopia : The Liang Barsky line clipping algorithm in a nutshell
このソースコードを参考に、プチコン3号で線分のクリッピングを行う関数を作ったのが以下のリストです。
DEF CLIPLINE(A_LINE,LEFT,TOP,RIGHT,BOTTOM) VAR I,T0,T1,DX,DY,P,Q,R DX=A_LINE[2]-A_LINE[0] DY=A_LINE[3]-A_LINE[1] T0=0:T1=1 FOR I=0 TO 3 IF I==0 THEN P=-DX:Q= A_LINE[0]-LEFT IF I==1 THEN P= DX:Q=-A_LINE[0]+RIGHT IF I==2 THEN P=-DY:Q= A_LINE[1]-TOP IF I==3 THEN P= DY:Q=-A_LINE[1]+BOTTOM IF P==0 THEN IF Q<0 THEN RETURN FALSE CONTINUE ENDIF R=Q/P IF P<0 THEN IF R>T1 THEN RETURN FALSE T0=MAX(R,T0) ELSEIF P>0 THEN IF T0>R THEN RETURN FALSE T1=MIN(R,T1) ENDIF NEXT A_LINE[2]=A_LINE[0]+ROUND(T1*DX) A_LINE[3]=A_LINE[1]+ROUND(T1*DY) A_LINE[0]=A_LINE[0]+ROUND(T0*DX) A_LINE[1]=A_LINE[1]+ROUND(T0*DY) RETURN TRUE END
最初のパラメータは長さ4の配列で、クリッピングしたい線分の座標をX0,Y0,X1,Y1の順に格納します。
続く4つのパラメータがクリッピングするための矩形です。
座標軸はX軸が右向き、Y軸が下向きと考えて、矩形の左上の座標が(LEFT,TOP)、右下の座標が(RIGHT,BOTTOM)です。
クリッピングした結果は第一引数の配列に格納されます。
描画するものが無い場合はFALSE、描画するものがある場合はTRUEが返り値になります。
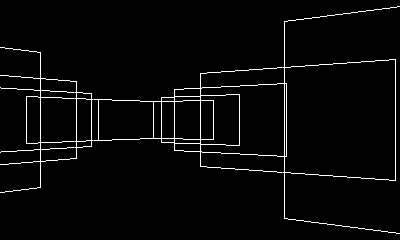
これで、安心して擬似3DでGLINE命令を使えますので、ちょっとしたデモプログラムを作ってみました。
この記事の最初の画面写真がそれです。
床面に10×10の格子を描き、立方体を5つ配置しました。
さらに、スプライトを1つ、円周上に動かしています。
上から見ると以下のような感じです。円はスプライトの軌跡です。
まずプログラムのメイン部分です。
DEF ROTATE X,Y,T OUT X1,Y1 X1=COS(T)*X - SIN(T)*Y Y1=SIN(T)*X + COS(T)*Y END ACLS DIM X[100],Z[100] FOR I=0 TO 99 X[I] = -1800 + 400*(I MOD 10) Z[I] = -1800 + 400*FLOOR(I / 10) NEXT SPSET 0,3088 SPANIM 0,"I+",10,0,10,1,10,2,10,3,0 SPOFS 0,200,120 SP_T=0:SP_U=0:SP_V=0:SP_W=0 T=0:U=0:V=0:W=0 DIM R_X[100],R_Z[100] PAGE=0 @LOOP GPAGE PAGE,(PAGE+1) MOD 2 PAGE=(PAGE+1) MOD 2 B=BUTTON(0) IF B AND 256 THEN T=T-0.05 IF B AND 512 THEN T=T+0.05 IF B AND 1 THEN V=V-10 IF B AND 2 THEN V=V+10 STICK OUT DX,DY ROTATE DX,DY,-T OUT DX,DY U=U + DX*20 W=W + DY*20 FOR I=0 TO 99 ROTATE X[I]-U,Z[I]-W,T OUT R_X[I],R_Z[I] NEXT GCLS DRAW_SCENE R_X,R_Z SP_T=SP_T+.1 ROTATE 500,0,SP_T OUT SP_U,SP_W SP_V=-300+50*SIN(SP_T*5) ROTATE SP_U-U,SP_W-W,T OUT SP_U,SP_W IF SP_W >0 THEN SCALE=SCALE_Z(SP_W) SP_X=SP_U*SCALE+200 SP_Y=(SP_V-V)*SCALE+120 SPSCALE 0,SCALE*6,SCALE*6 SPOFS 0,SP_X,SP_Y,0 SPSHOW 0 ELSE SPHIDE 0 ENDIF VSYNC 1 GOTO @LOOP
赤い部分がスプライトのための処理です。
コウモリのキャラクタを設定し、アニメーションも付けています。
3次元空間の中でのスプライトの座標を計算するために変数(SP_U,SP_V,SP_W)を使います。
また、このスプライトは原点を中心とした円周上を飛ばします。
円周上の位置は角度SP_Tで表します。
ループに入る前後のところで
PAGE=0 @LOOP GPAGE PAGE,(PAGE+1) MOD 2 PAGE=(PAGE+1) MOD 2
というコードがありますが、これは画面のダブルバッファの処理です。
今回は描画処理が重く、そのままではちらつくので、GPAGEで表示ページと描画ページに別のページを指定し、描画処理が終わったら2つのページを入れ替えるようにしています。
背景をGLINEで描く部分は、DRAW_SCENEとして別関数に分けています。
DRAW_SCENEのパラメータとして、視点の回転による座標変換を行った後のX座標とZ座標の配列を渡しています。
座標の個数はそれぞれ100個で、10×10の格子状に並んでいます。
その後が、スプライトを回転移動させるための処理です。
まずSP_Tを0.1ラジアン増やします。
そして、(500,0)をSP_Tだけ回転した座標をSP_U,SP_Wに代入します。
Y座標であるSP_Vは、-300を基準として、sin関数でゆらゆらと上下に動かしています。
以上でスプライトの(空間内での)座標が決まり、こんどはそれをスクリーンからの相対座標に変換します。
これは前回・前々回で行ったのと同じ処理です。
そして、変換後のZ座標が正なら、縮小率を計算してスクリーン上での表示位置を決定し、スプライトのスケールや位置を指定します。
Z座標が負ならスプライトを消します。
関数SCALE_Zは縮小率を求める関数です。
DEF SCALE_Z(Z) RETURN 400/(400+1600*(Z/2000)) END
では、先ほど青字で示した、背景のワイヤーフレーム描画の処理です。
以下のGLINE3Dが、一番基本的な、3次元空間での線分描画を行います。
(X0,Y0,Z0)から(X1,Y1,Z1)まで、色Cで線分を描きます。
X,Z座標値はカメラの向きに応じて回転した後の座標値が必要です。
また、パラメータで与えていませんが、現在のスクリーンの位置に関する変数「V」をY座標の計算に使っています。
DEF GLINE3D X0,Y0,Z0,X1,Y1,Z1,C VAR S0,S1,X2,Y2,X3,Y3 DIM L[4] L[0]=X0 L[1]=Z0 L[2]=X1 L[3]=Z1 IF !CLIPLINE(L,-9999,-1,9999,19999) THEN RETURN S0=SCALE_Z(L[1]) S1=SCALE_Z(L[3]) L[0]=L[0]*S0+200 L[2]=L[2]*S1+200 L[1]=(Y0-V)*S0+120 L[3]=(Y1-V)*S1+120 IF CLIPLINE(L,0,0,400,240) THEN GLINE L[0],L[1],L[2],L[3],C ENDIF END
GLINE3Dは座標を全て与えなければなりませんので、X座標の配列とZ座標の配列を使って、XZ座標を番号で指定できるようにPGLINE3Dを定義しています。
DEF PGLINE3D P1,Y1,P2,Y2,C,X,Z GLINE3D X[P1],Y1,Z[P1],X[P2],Y2,Z[P2],C END
PGLINE3Dを使って直方体を描画する関数DRAW_CUBEです。
DEF DRAW_CUBE P1,P2,P3,P4,Y1,Y2,C,X,Z PGLINE3D P1,Y1,P2,Y1,C,X,Z PGLINE3D P2,Y1,P3,Y1,C,X,Z PGLINE3D P3,Y1,P4,Y1,C,X,Z PGLINE3D P4,Y1,P1,Y1,C,X,Z PGLINE3D P1,Y2,P2,Y2,C,X,Z PGLINE3D P2,Y2,P3,Y2,C,X,Z PGLINE3D P3,Y2,P4,Y2,C,X,Z PGLINE3D P4,Y2,P1,Y2,C,X,Z PGLINE3D P1,Y1,P1,Y2,C,X,Z PGLINE3D P2,Y1,P2,Y2,C,X,Z PGLINE3D P3,Y1,P3,Y2,C,X,Z PGLINE3D P4,Y1,P4,Y2,C,X,Z END
以下がDRAW_SCENEの本体です。
GLINE3DとDRAW_CUBEを呼んでいるだけです。
DEF DRAW_SCENE X,Z VAR C,I C=&HFFFFFFFF FOR I=0 TO 9 GLINE3D X[I],120,Z[I],X[90+I],120,Z[90+I],C GLINE3D X[I*10],120,Z[I*10],X[I*10+9],120,Z[I*10+9],C NEXT GLINE3D X[99],120,Z[99],X[9],120,Z[9],C GLINE3D X[90],120,Z[90],X[99],120,Z[99],C C=&HFFFFFF00 DRAW_CUBE 7,8,18,17,120,-240,C,X,Z DRAW_CUBE 92,93,83,82,-300,-560,C,X,Z C=&HFFFF00FF DRAW_CUBE 97,98,88,87,120,-240,C,X,Z DRAW_CUBE 1,2,12,11,-400,-600,C,X,Z C=&HFF00FFFF DRAW_CUBE 12,14,24,22,120,-800,C,X,Z END
以上で、擬似3Dの背景をグラフィックスで描くことができました。
とはいえ、ワイヤーフレームではやっぱりちょっと寂しい感じもします。
プチコン3号の先日のアップデートで、三角形を描く命令GTRIが新たに追加されましたので、次回はGTRIを使ってポリゴンで描く擬似3Dプログラムを作ります。






コメント