プチコン３号　１４日目　グラフィックスとアニメーション

2015/01/12

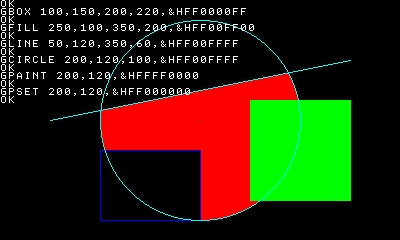
プチコン３号にはスプライトやＢＧ以外に、画面に直接絵を描く命令もあります。
描ける図形は
・矩形（線幅１ピクセル、塗りつぶし無し）
・矩形（塗りつぶし）
・直線（線幅１ピクセル）
・真円（線幅１ピクセル、塗りつぶし無し）
・点（１ピクセル）
の５種類で、さらに
・領域塗りつぶし（領域の境界の色指定可）
も可能です。
多角形や楕円、太い線などは描けません。
命令は、ダイレクトモードから簡単に試すことができます。

pc14-1.jpg

これらの命令の実行速度は結構速いので、スクリーンを消しては絵を描き、を繰り返すと、描いた絵を動かすことができます。
そこで、ボールを床に落とすと弾むような感じで、円がスクリーンの中を弾んで動くアニメーションを作ってみました。

pc14-2.jpg

１１個のボールがポンポン弾みながら画面の中を動きます。

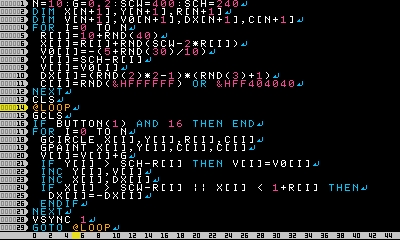
プログラムリストはこちらです。

pc14-3.jpg
N=10:G=0.2:SCW=400:SCH=240
DIM X[N+1],Y[N+1],R[N+1]
DIM V[N+1],V0[N+1],DX[N+1],C[N+1]
FOR I=0 TO N
R[I]=10+RND(40)
X[I]=R[I]+RND(SCW-2*R[I])
V0[I]=-(5+RND(30)/10)
Y[I]=SCH-R[I]
V[I]=V0[I]
DX[I]=(RND(2)*2-1)*(RND(3)+1)
C[I]=RND(&HFFFFFF) OR &HFF404040
NEXT
CLS
@LOOP
GCLS
IF BUTTON(1) AND 16 THEN END
FOR I=0 TO N
GCIRCLE X[I],Y[I],R[I],C[I]
GPAINT X[I],Y[I],C[I],C[I]
V[I]=V[I]+G
IF Y[I] > SCH-R[I] THEN V[I]=V0[I]
INC Y[I],V[I]
INC X[I],DX[I]
IF X[I] > SCW-R[I] || X[I] < 1+R[I] THEN
DX[I]=-DX[I]
ENDIF
NEXT
VSYNC 1
GOTO @LOOP

今回のプログラムは、比較的簡単な内容です。
最初に定数の宣言です。

N=10:G=0.2:SCW=400:SCH=240

Nは円の個数－１、Gは加速度、SCWはスクリーンの横方向のピクセル数（Width）SCHはスクリーンの縦方向のピクセル数（Height）です。
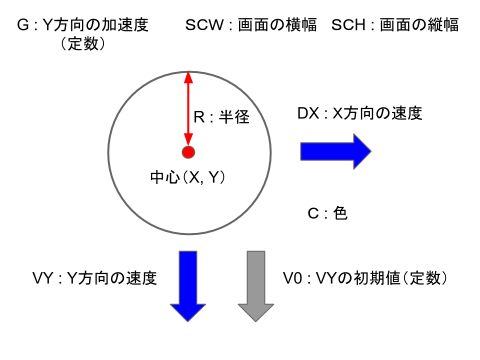
次に、円を表すために必要なパラメータを、円の個数分、配列で宣言しています。
各変数の意味は、下図を見てください。

初期化時に、各円のY座標は画面下部に接する位置（床に接触した状態）とし、VYの初期値V0を上方向にランダムに与えています。
このV0が、床から跳ね返って上に向かう瞬間の初速になります。

X軸方向の移動量は、-1, 1のいずれか(RND(2)*2-1)をランダムに決め、さらにそれを１～３倍(RND(3)+1)しています。

pc14-4.jpg

ループの中では、まずGCLSで画面全体を消去します。
次にボタンの状態をチェックして、Aボタンが押されていればプログラム終了です。

そのあと、各ボールの処理をするループになります。
まずGCIRCLEで円を描き、GPAINTでその中を塗りつぶします。
境界色をGCIRCLEの色指定と同じ色にしていますので、他の描画済みの円があっても上書きします。

次にＹ座標の計算です。
まず、Ｙ方向の速度VYに重力を表す加速度Gを加算します。
落下速度が時間につれて大きくなっていきますので、円の動きは下方向に向かって加速していきます。
この様子は下図を見てください。
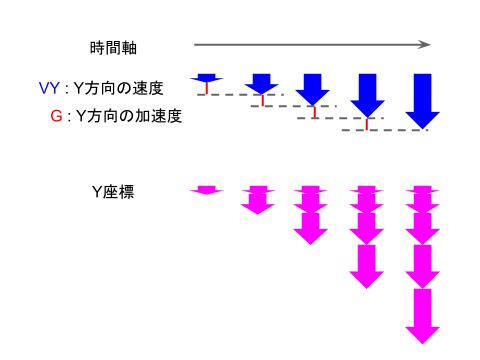
pc14-5.jpg
そのあと、現在のＹ座標をチェックし、円の下端がスクリーンの下端を超えていたら、VYを初期値であるV0にリセットします。
V0は画面上方向に向かう初速ですので、これで円が床から上に跳ね上がります。

この部分ですが、物理法則から考えると

VY=-VY

としても良さそうに思えます。
しかし、今回は速度を整数ではなく浮動小数で表しているため、演算の際の計算誤差の問題があって、跳ね返るたびにだんだんVYの絶対値が小さくなっていってしまいます。

その後はＸ座標の計算ですが、こちらは座標が整数値ですので、画面の左右端でDXの符号を反転させるだけです。

今回のプログラムですが、Nの値をいろいろ変えてみると、１８個（N=17）までは画面がちらつかずに描画することができました。
塗りつぶした円を描く命令が無いので、GCIRCLEとGPAINTを組み合わせて描きましたが、それでもかなり速いですね。

なお、プログラムの中身は大きく変えずに命令の実行順序を変えれば、さらにちらつきを少なくすることができます。
ループの中のFOR～NEXT文で、円１つずつ、描画と座標の計算をしていますが、ここを２つのFOR～NEXTループに分解して、まず全部の円を描画し、その後で全部の円の座標の計算をするように変更すると、２１個（N=20）まで描けました。

コメント