前回作成した「迷路探検ゲーム」のプログラムは、迷路生成には5日目に作成したプログラムを使っています。
5日目のプログラムで使用したアルゴリズムは、「バイナリーツリー法」と言います。
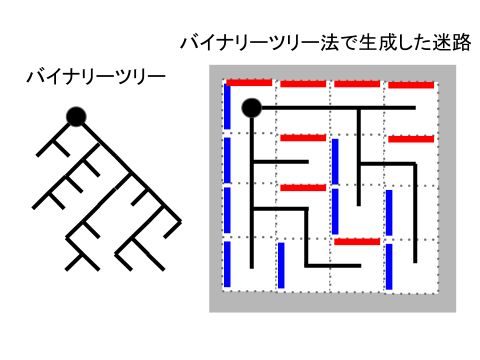
バイナリーツリー(二分木)とは、枝が二又に分かれる木のようなデータ構造です。
バイナリーツリー法で生成した迷路は、その経路がスタート地点を根とし、右または下方向だけに伸びていくバイナリーツリーになります。
下図を見れば、実際そうなっていることが解るでしょう。
さて、バイナリーツリー法の迷路は、欠点があります。
その話の前に、「良い迷路」とはどういうものかを考えてみましょう。
一言で言えば、「一見して正解が判りづらいもの」ということになると思います。
下図を見てください。
迷路のすべての通路に紐を置き、それらを各部屋の中央で結んでツリー構造を作ります。
そして、スタート地点とゴール地点をつかんで引っ張り、まっすぐに伸ばしたと考えます。
すると、図の左の迷路は図の右のように表せます。
良い迷路とは、このように正解を中央の一本道で表現したとき、
・正解の道が短すぎず、
・正解の道からの脇道が少なすぎず、
・脇道が正解に比べて短すぎない
というような迷路だと考えることができます。
例えば図(A)のような迷路は、脇道は多いが短すぎるため、すぐ袋小路に行き当たってしまいます。
また図(B)のような迷路は、脇道は複雑ですが肝心の正解が短いため、すぐゴールへ到達してしまう可能性があります。
ではバイナリーツリー法で作られた迷路はどうでしょうか?
このアルゴリズムでは、正解の道の長さは「迷路の幅+迷路の高さ」が最大です。
なぜならUターン、つまり連続して2回右へ曲がったり、連続して2回左へ曲がることができないからです。
これは「北か西、どちらかの壁を残す」というルールから来ています。
Uターンするような経路を作ろうとしたら、このルールを満たさない部屋が必要になります。
正解の道の長さ、脇道の長さ、共にあまり長くすることができないのはバイナリーツリー法の欠点です。
また、上で述べたとおりUターンするような経路が作れないことも問題です。
というわけで、今回は5日目の記事よりも良い迷路を生成するアルゴリズム「リカーシブ・バックトラッカー法」による迷路生成プログラムを作ってみました。
5日目の記事でも紹介しましたが、以下のリンクで様々な迷路生成アルゴリズムが解説されています。
"Algorithm" is Not a Four-Letter Word
「リカーシブ・バックトラッカー法」は、その中でも比較的、簡単に良い迷路を生成するアルゴリズムです。
これは、以下のようなルールで迷路を作ります。
(1)現在地の部屋は、元来た部屋へ向かう以外の方向はすべて壁があると考える。
(2)現在地のすぐ隣の部屋で、まだ訪れていない部屋を(ランダムに)選び、壁を壊してその部屋へ進む。
(3)もし周囲が全て訪れたことのある部屋ならば、来た道をひとつ引き返す。
(4)再び(1)から始める。
これを繰り返すと、最終的に全ての部屋を回り終えた後、出発点の部屋にまで戻ってきます。
それ以上は引き返せませんので、これで迷路が完成です。
ちなみに「リカーシブ」とは再帰的、すなわちある作業をより簡単な作業に分解すると、その中に再び同じ作業が含まれているような性質を指します。
また「バックトラック」とは、来た道をなぞって戻っていくようなイメージです。
今回は、この「リカーシブ・バックトラッカー法」による迷路生成プログラムを作ってみました。
基本的なデータ構造は5日目と同じです。
すなわち、部屋が縦横に規則正しく並んでいて、各部屋は「西」と「北」に壁があるものと考えます。
また、迷路の周囲を「入れない部屋」が取り囲んでいて、壁を壊してその部屋へ進むことはできないものとします。
上記を二次元配列を使って表現する点も同じです。
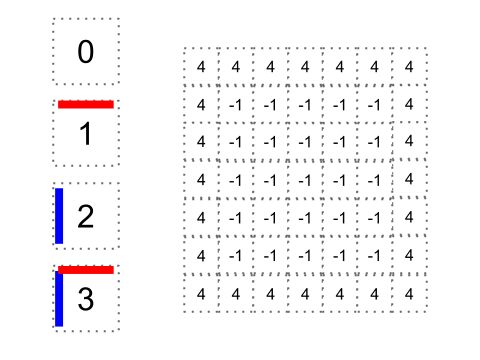
ただし、今回は「西の壁と北の壁の両方が無い部屋」もありえますので、部屋の壁の状態と、配列の数値との対応は
・北、西に壁:3
・北に壁:2
・西に壁:1
・壁無し:0
・未訪問:-1
・入れない:4
というように変更します。
迷路の初期状態は、すべての部屋が「-1」で、その周囲を「4」の部屋が取り囲んでいます。
「リカーシブ・バックトラック法」では、進めなくなったらどんどん後戻りしますので、元来た部屋をすべて記録しておく必要があります。
そのために「スタック」を使います。
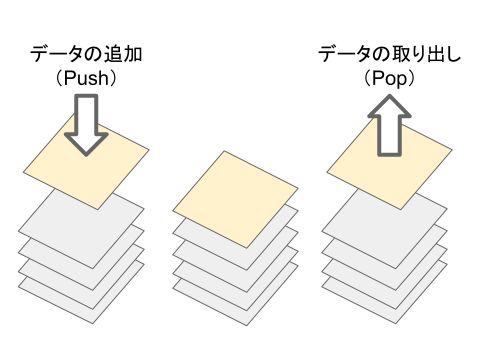
スタック(Stack)とは積み重ねたものという意味ですが、その名の通り、データを追加するときは古いデータの上に新しいデータを積み重ねます。
そして、データを取り出すときは、新しいデータから取り出していきます。
積み重ねる操作を「Push」、取り出す操作を「Pop」と言います。
未訪問の部屋へ移動するときは、今いる部屋の座標をスタックへ「Push」します。
そして、後戻りするときは、戻るべき部屋の座標をスタックから「Pop」します。
SmileBASICでは、配列をスタックのように扱う命令「PUSH」「POP」が用意されていますので、今回はこれを使います。
なおSmileBASICの「PUSH」「POP」命令は、DIMで宣言した配列のサイズを超えた場合には配列のサイズを自動で大きくします。
(なお「リカーシブ」なプログラムの書き方としては、関数定義の中でその関数自身を呼び出すやり方が有名です。SmileBASICも、DEF文を使ってそのような関数定義が書けます。
ただ、残念なことに現在のバージョンのSmileBASICは再帰呼び出しできる回数に制限があり、それを超えるとエラーになってしまいます。具体的には、千数百回程度が限界のようです。
迷路の経路の最大の長さをこの回数が以下にしないとエラーになってしまいます。エラーにならない迷路のサイズは、目安としては50×50程度までです。
40×40の迷路でも1600部屋ありますから、脇道無しならエラーになる可能性があります。
そのため、今回は再帰呼び出しではなく、ループとスタックを使ってプログラムを実現しています。)
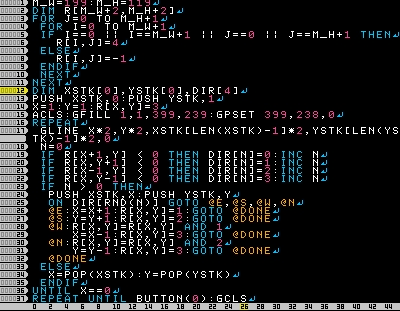
それではプログラムリストです。
M_W=199:M_H=119 DIM R[M_W+2,M_H+2] FOR J=0 TO M_H+1 FOR I=0 TO M_W+1 IF I==0 || I==M_W+1 || J==0 || J==M_H+1 THEN R[I,J]=4 ELSE R[I,J]=-1 ENDIF NEXT NEXT DIM XSTK[0],YSTK[0],DIR[4] PUSH XSTK,0:PUSH YSTK,1 X=1:Y=1:R[X,Y]=3 ACLS:GFILL 1,1,399,239:GPSET 399,238,0 REPEAT GLINE X*2,Y*2,XSTK[LEN(XSTK)-1]*2,YSTK[LEN(YSTK)-1]*2,0 N=0 IF R[X+1,Y] < 0 THEN DIR[N]=0:INC N IF R[X,Y+1] < 0 THEN DIR[N]=1:INC N IF R[X-1,Y] < 0 THEN DIR[N]=2:INC N IF R[X,Y-1] < 0 THEN DIR[N]=3:INC N IF N > 0 THEN PUSH XSTK,X:PUSH YSTK,Y ON DIR[RND(N)] GOTO @E,@S,@W,@N @E:X=X+1:R[X,Y]=1:GOTO @DONE @S:Y=Y+1:R[X,Y]=2:GOTO @DONE @W:R[X,Y]=R[X,Y] AND 1 X=X-1:R[X,Y]=3:GOTO @DONE @N:R[X,Y]=R[X,Y] AND 2 Y=Y-1:R[X,Y]=3:GOTO @DONE @DONE ELSE X=POP(XSTK):Y=POP(YSTK) ENDIF UNTIL X==0 REPEAT UNTIL BUTTON(0):GCLS
1行目で、迷路のサイズを決めています。
今回は迷路の描画にはグラフィックスを使い、400ドット×240ドットの画面の2×2ドットで迷路の1部屋を表現することにしました。
それに合わせて、画面全体を迷路にする199×119という巨大迷路にしています。
最初の配列の初期化処理は、5日目のときとほぼ同じです。
ただし、先に説明したように、初期値は壁が「4」それ以外が「-1」となっています。
12行目で、座標を格納するスタックのための配列XSTK、YSTKと、進むことができる方向を記録するための配列DIRを宣言しています。
そして、スタックに座標(0,1)をプッシュしていますが、これは座標ではなくて「スタックが空である」ことの目印のために使います。
迷路の中の座標でX=0となるのは迷路の周囲の壁だけであり、迷路の中の座標でXがゼロになることはないからです。
スタート地点は(1,1)とし、その部屋を訪問済みにしています。壁は西・北とも「あり」の状態です。
そして、REPEAT~UNTILのループで迷路の全ての部屋を訪問します。
ループから抜けられるのはX==0のときですが、この条件が満たされるのは13行目でスタックにプッシュした0がポップされたときだけです。
まず、現在の部屋の上下左右の部屋が訪問済みかどうかチェックし、未訪問ならその方向を配列「DIR」に追加します。
方向は、東・南・西・北をそれぞれ0,1,2,3で表します。
Nには、DIRに格納されている方向の個数が入ります。
(実はDIRもスタックにしても良かったのですが、スタックを簡単に空にする命令が見当たらなかったので止めました。)
そして、未訪問の部屋が1つ以上ある場合は、まず現在地をスタックにプッシュします。
次いで
DIR[RND(N)]
で、未訪問の方向を1つ、ランダムに選び、その方向に進みます。
進んだ先の部屋では、進行方向と整合するように北・西の壁の設定をします。
たとえば東の部屋へ進んだら、進んだ先の部屋に西の壁があるのはおかしいので、「北の壁のみあり」の状態にします。
西に進む処理で
R[X,Y]=R[X,Y] AND 1
という処理をしていますが、これは「現在いる部屋の西の壁を取り払う(北の壁は、あっても無くても現状維持)」ことを表します。
同様に北に進む処理では、現在いる部屋の北の壁を取り払います。
未訪問の部屋がひとつも無かった(N==0)場合は、スタックからX,Yをひとつ取り出し、そこへ移動します。
(つまり、来た道を1つ引き返す。)
スクリーンいっぱいの迷路ですが、けっこうあっという間に作成が終わります。
やはり、BASICとはいえ昔のマシンとは違いますね。
そもそも昔の8ビット機だったら、200×100の配列を使うプログラムなんて、ちょっと使うのがドキドキするようなメモリ食いのプログラムだったと思います。





コメント