今回は、前回までの内容を使って鋸波のオシレータを作ってみます。
なおコードは以下で公開しています。
前回書いたように、logue SDKでは鋸波のウエーブテーブルが提供されていますが、テーブル数は7つと少なめです。
実際にlogue SDKのウエーブテーブルで作った鋸波を鳴らしてみると、特にC6~B7のあたりで倍音成分が不足しています。この範囲は、インデックス番号5とインデックス番号6のウエーブテーブルをミックスして生成されています。
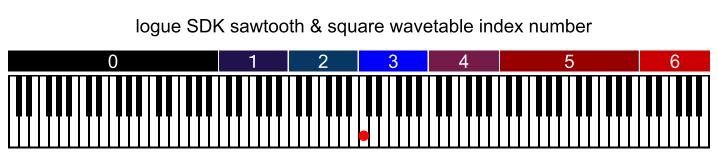
この範囲で最も倍音数が多い(周波数が低い)C6の倍音数は22(24000/1046.5)、もう1つ上のウエーブテーブルはC8からで、倍音数は5です。つまり、5~22という倍音数の範囲を2つのウエーブテーブルの補間で生成していることになります。
いろいろ音を鳴らしながらスペクトルを見た印象だと、logue SDKの鋸波や矩形波のウエーブテーブルは、再生できる限界である24KHzで倍音成分をばっさり切っていません。むしろ、限界に近づくにつれて倍音の係数が0に近づくように調整されているのではないかと思います。補間を滑らかにするための工夫かもしれませんが、結果的に倍音成分を弱くしています。
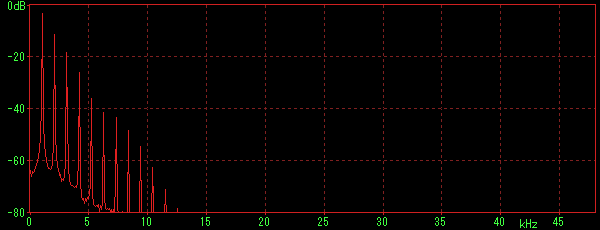
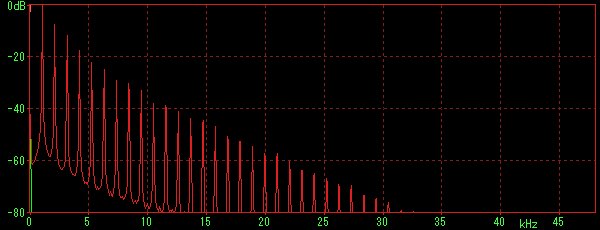
上は、NTS-1にデフォルトで入っているSAWでC6を鳴らしたときのスペクトルです。きれいにスペクトルが下がっていますが、下がり方が急峻です。下のαJunoのC6のスペクトルと比べてみると分かります。
今回作るオシレータではテーブル数を大幅に増やし、かつ倍音成分もできるだけカットしないものを作ってみます。下のスペクトルが、今回作成したオシレータでC6を鳴らしたときのものです。
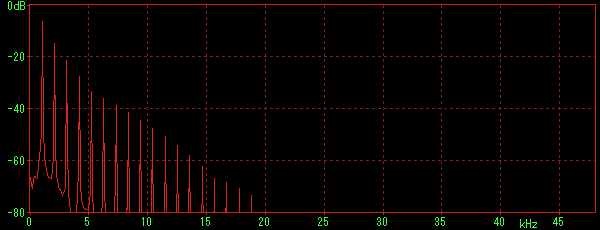
とはいえ、logue SDKではコードとデータを合わせて32KB以内という制約がありますので、テーブルを大幅に増やすといっても限度があります。Synth1のDaichiさんが公開されているVSTプラグインのサンプルでは、1024サンプルのテーブルを68個も使用していますが、これをlogue SDKで実現するのは難しいです。
今回は、32KBに納めるために以下のような設計としました。
・波形は対称性があるので、サンプルは半波長分だけ用意する
・テーブル1つのサイズは128サンプル=512バイトとする
この条件で計算してみますと、51個(約25KB)のテーブルで全ての音高をカバーできます。ただし波長あたり256サンプルなので、128倍音までの音しか含みません。128倍音以上が必要となるF#3以下の音階も、128倍音のデータを使います。ですので、低いほうの音は「若干、キレが足りない」と感じるかもしれません。
51個のウエーブテーブルの作成は、以下の式で表される鋸波のフーリエ級数展開をPythonで計算して行います。
$$y{(t)}=\frac{2}{\pi}\sin(t)+\frac{2}{\pi}\frac{\sin(2t)}{2}+…+\frac{2}{\pi}\frac{\sin(kt)}{k}+…$$
作成したPythonスクリプトはこちらです。処理の流れだけ書くと、以下のようになっています。
(1)生成したいノート番号の範囲のリストを作る。今回は24(C1)から138(24KHz以下での最高音)まで。(C1より低い音は倍音数が多すぎるので、最初から対象外としました)
[24, 25, 26, … ,137, 138]
(2)各ノート番号の倍音の次数を計算し、(ノート番号,次数)というタプルのリストを作る。
[(24, 128), (25, 128), … , (137, 1), (138, 1)]
(3)(2)のリストの次数の部分だけを取り出してユニークな次数のリストを作る。
[128, 127, 120, 113, … , 4, 3, 2, 1]
(4)(3)と(2)の結果を使って、{次数:ノート番号のリスト}の辞書を作る。
{128:[24,25,…,50], 127:[51], 120:[52], … ,1:[117, 118, … ,138]}
(5)(4)の辞書を使って、各次数の最大のノート番号を調べ、リスト化する。
[50, 51, 52, … , 111, 116, 138]
(6)(5)の結果を、テーブルのインデックス番号の決定用に出力する。
(7)(4)の各次数についてテーブルを生成して出力する。
このスクリプトを走らせると、生成した50個の内の一部の波形を最後に表示します。その結果が以下のグラフです。nは何次の倍音まで加算したかを表します。
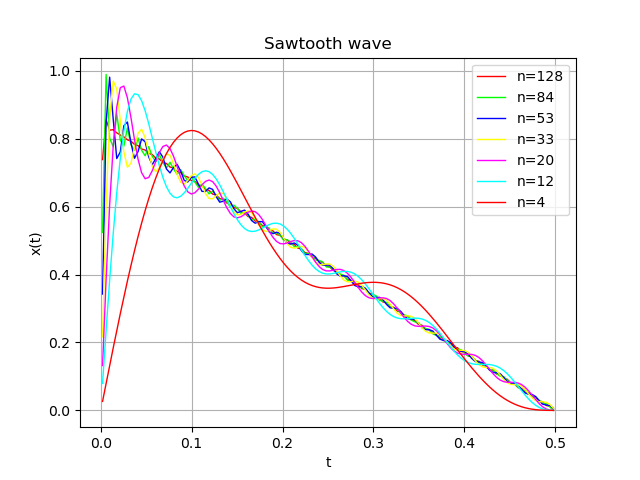
グラフを見ると分かるように、倍音の個数によっては左上の部分に尖った角のような波形が出ます(Gibbs現象)。logue SDKでは波形の信号を-1.0~1.0の固定小数点数に変換しますので、この範囲に値を納めるように、実際の計算では前述のフーリエ級数に1より小さい係数を掛けています。
Gibbs現象は倍音を無限個ではなく有限個しか加算していないために起こります。高次の倍音を切り捨てると、それより少し低次の倍音が打ち消されなくなり、波形上で目立つためです。これを避けるには、それぞれの倍音成分に対して、次数が高くなるほど値が小さくなるような係数を掛ける方法があります。たとえばこちらで解説されている手法は、係数に$$\cos^2(n-1)k$$を掛けます。nが次数、kは\(\pi/2\)を倍音の個数で割ったものです。最も低い倍音では\(n=1\)なのでこの係数は1です。次数が上がると\(\cos\)のパラメータが\(\pi/2\)に近づいていくので、値はゼロに近づきます。倍音の次数が上がるほど音量が下がるので、音色は倍音成分が少ないダークな傾向に振れます。この手法はlogue SDKの内蔵のウエーブテーブルの音色傾向に近づいてしまうので、今回は使っていません。
実装に関して、一点だけ気をつけなければいけないのは、ウエーブテーブルの時間軸の取り方です。
今回、サンプリングデータは波長の前半だけしか作成しません。波長の後半は、下図のように前半のデータを後ろから前に読み進め、符合を反転して作成します。
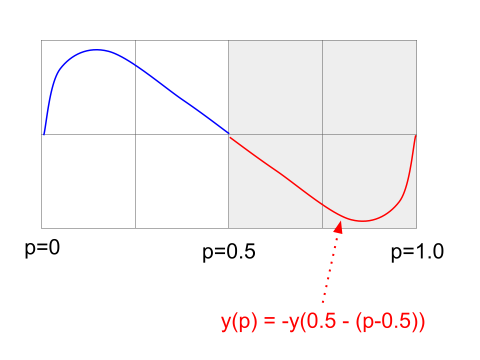
このとき、サンプルデータが偶数個で下図の赤いポイントの位置で計算されていると、時間軸方向に反転したときにサンプルの間隔がずれてしまいます。サンプルは図の緑のポイントの位置で計算し、折り返してもポイントの間隔を一定にしておく必要があります。
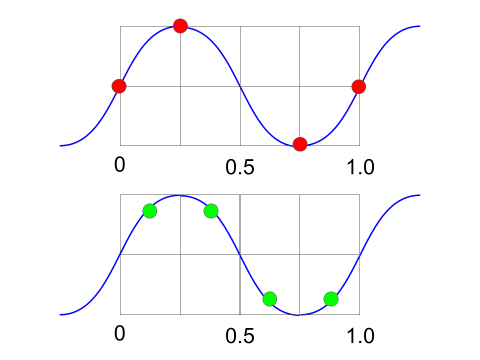
作成したPythonスクリプトのウエーブテーブル生成部分はは以下のようになっています。max_phi / table_sizeがサンプルの間隔で、その1/2だけ時間軸をずらしています。
# generate wavetables
t = np.linspace(0., max_phi, table_size, endpoint=False)
t += max_phi / table_size / 2
wave_tables = []
for h in harmonics:
wt = np.zeros(shape = (t.shape[0],),)
for n in range(1, h + 1):
wt += max_value * 2/(np.pi * n) * np.sin(2 * np.pi * n * t)
wave_tables.append(wt)
最後にNTS-1で、最初から内蔵されているSAWと、今回作成したオシレータで鳴らした音を載せておきます。
こちらが今回作成したものです。
次に、NTS-1の内蔵のSAWです。おそらくlogue SDKで提供されているウエーブテーブルを使っていると思います。
比べると、ローパスフィルタを掛けたように音が暗くなっているのがわかるでしょうか。ノイズが出なくて使いやすくはありますが、ちょっと物足りないのではと思います。

コメント