前回はエイリアスノイズの出ない鋸波を、ウエーブテーブルを使って生成しました。
この方法の欠点は、沢山のウエーブテーブルが必要になる点です。
PCのソフトシンセでは問題になりませんが、logue SDKではデータとコード合わせて32KBしか使えませんので、音質も考慮した十分なウエーブテーブルを用意することは難しいです。
そこで、ウエーブテーブルを使わず、かつエイリアスノイズも出ない「BLIT」による波形合成を試してみます。
BLITについては、あのSynth1のDaichiさんが少し触れられている他、日本語で読めるものとしては以下のようなものがあります。
英語で良ければ以下が解りやすいと思います。

簡単に説明すると、(鋸波の)BLITとは以下のようなものです。
(1)鋸波の波形を、ウエーブテーブルではなく、直前のサンプルからの「差分」を加算する(つまり、y = wavetable[x]ではなく、y = y + delta[x]で波形を求める)ことで合成する。
(2)鋸波では、波形が不連続に変化する点があるので、(1)の「差分」はその不連続な変化点で短いピーク(Impulse)が現れる。
(3)サンプリング周波数の1/2を超えないように波形を生成するには、この差分の信号もサンプリング周波数の1/2を超えないようにする(Band-Limited)必要がある。
(4)Band-LimitedなImpulseが繰り返し出現する信号をBLIT=Band Limited Impulse Trainと呼ぶ。
適切なBLIT波形が得られれば、それを積分(コードとしてはy = y + blit(x)をループ)していくことでエイリアスノイズの出ない鋸波が得られます。正確には、BLITを積分して得られるのは波形の中の階段状の部分で、これに波形の中のなだらかな部分として\(y=-kx(ただしkは波長の逆数)\)を加えることで鋸波になります。
では、そのBLIT波形はどのような波形かというと、\(n\)番目のサンプルの値\(y(n)\)は
$$y(n) = (M/P) Sinc{_M}[(M/P)n]\\ \\
ただし Sinc{_M}(x) = \frac{\sin(\pi x)}{{M \sin(\pi x/M)}}$$
という式で表されます。(式の導出は上記の2番目のリンク先にあります)
う~ん、ぴんと来ませんね?
まず、\(Sinc\)関数という関数があります。これは
$$Sinc(x) = \frac{\sin(x)}{x}$$
という関数で、こんな形をしています。(画像はWikipediaより)
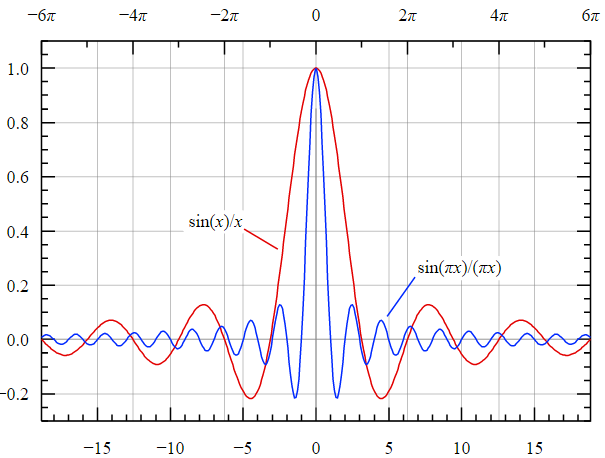
\(Sinc\)関数は中央が値が大きく、両側では値が小さくなります。分母が\(x\)だからですね。そして、ピークでは分子・分母とも0ですが、ピークの値は不定値ではなく解析的に求まります。
一方、\(Sinc{_M}\)関数は分母が\(\sin(x/M)\)ですので、分母も振動し、ピーク(分子・分母ともに0となる)が周期的に現れます。
また、このときMが奇数なら、分子と分母が同じ符合で強め合うため、値が大きくなる部分は常に正となります。
Mが偶数なら、値が大きくなる部分は正と負が交互に現れます。
鋸波の生成では、Mが奇数の場合だけを扱います。ちなみにMが偶数の場合は、矩形波を生成できます。
下図が\(Sinc{_M}\)関数をプロットした例です。緑はMが偶数、赤はMが奇数の例です。
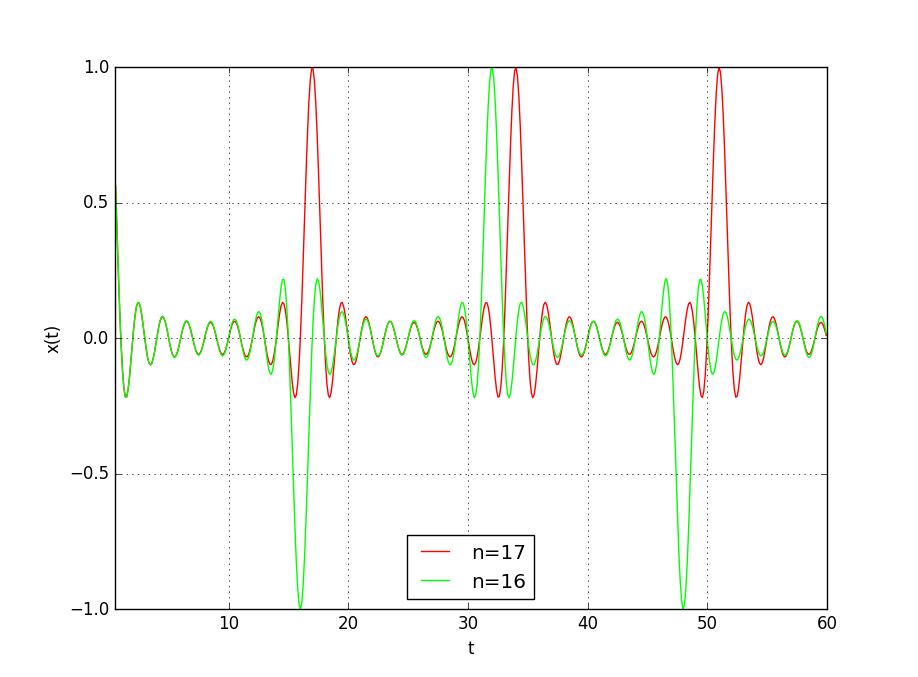
あと、上の式で出てくる\(P\)と\(M\)は何か? ですが、
・\(P\)は生成する鋸波のサンプル数
・\(MはP\)を超えない奇数で、BLIT信号に含まれる最大の倍音の次数
を表します。
実際には、サンプリング周波数を\( f_{s} \)、生成する音の周波数を\(f\)、倍音の次数を\(N\)とすると
$$ P = f_{s} / f \\
2Nf < f_{s} \\
2N < f_{s} / f = P $$
ですので、
$$ Pを超えない奇数 M=2N+1 $$
となります。
ちょっと長くなってしまったので、次回に続きます。次回は\(Sinc{_M}\)関数を積分して、実際に鋸波をプロットしてみます。
なお、上の\(Sinc{_M}\)関数をプロットするPythonのコードは以下の通りです。


コメント