前回、BLITについて簡単に説明しました。要約しますと、
・倍音成分をある周波数でカットした鋸波は、時間軸に沿ってBLITを積分すると生成できる。
・BLITは、以下の数式で表される。
$$y(n) = (M/P) Sinc{_M}[(M/P)n]\\ \\
ただし Sinc{_M}(x) = \frac{\sin(\pi x)}{M \sin(\pi x/M)}$$
ということでした。
今回は実際にBLITから鋸波を生成し、以前フーリエ級数で生成した波形
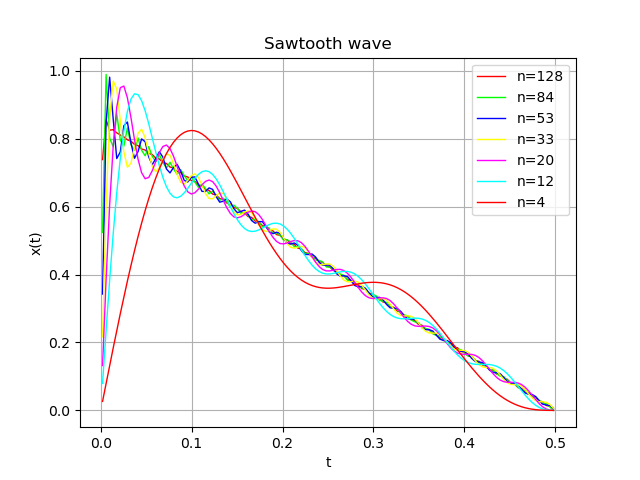
と同じものが得られることを確認します。
まず、最初に上の式を少し整理します。
$$y(n) = (M/P) Sinc{_M}[(M/P)n]\\
ただし Sinc{_M}(x) = \frac{\sin(\pi x)}{M \sin(\pi x/M)}$$
$$y(n) = (M/P)\frac{\sin(\pi (M/P)n)}{M \sin(\pi (1/P)n)} \\
= (1/P)\frac{\sin(\pi M(n/P))}{\sin(\pi (n/P))}
$$
ここで、\(P\)は波長あたりサンプル数で、\(n\)は何番目のサンプルなのかを表す数です。
\(n/P\)が表しているのは、1つの波長の中で、今どの位置を計算しているのかということを、先頭を0、末尾を1.0として表現したものになります。
そこで、\(\phi = n/P\)と置くと
$$y(n) = \frac{\sin(M\pi \phi)}{P\sin(\pi\phi)} $$
となります。だいぶスッキリしましたね。
ここで\(\phi\)は、logue SDKの使い方で説明したPhaseと同じです。
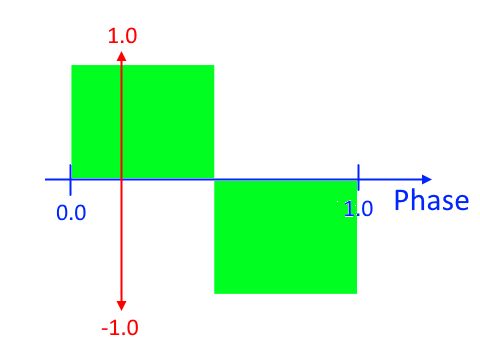
\(P\)は波長あたりサンプル数ですから、サンプリング周波数が\(f_s\)、生成したい音の周波数が\(f\)とすると、\(P=f_s/f\)です。
\(M\)は必ず奇数で、波形に含めたい最高次の倍音の次数を\(N\)とすると、\(M=2N+1\)です。
そして、\(M\)は\(P\)を超えてはいけません。\(P\)は1波長分のサンプルの個数を表していますので、要するにこれはサンプリング定理(サンプリング周波数が\(f_s\)のとき、再生可能な信号の周波数は\(f_s/2\)以下)と同じことを言っています。
\(M\)を大きくすればするほど理想的な鋸波に近づきます。ただし\(M\)は\(P\)より大きくできないので、より良い波形を得るには\(P\)も大きくする必要があります。そして\(P\)を大きくするとは、すなわちサンプリング周波数を上げるということです。
では、\(y(n)\)をプロットしてみましょう。最初にまず準備を。
import numpy as np
import matplotlib.pyplot as plt
def rgb(i):
b = (i & 4) >> 2
g = (i & 2) >> 1
r = i & 1
return (r, g, b)
colors = list(map(rgb, [1, 2, 4, 3, 5, 6]))
table_size = 512 # for a single wave
min_phi = 0.5 # plot from 0.5pi
max_phi = 2.5 # to 2.5pi
t = np.linspace(min_phi, max_phi, table_size, endpoint=False)
t += max_phi / table_size
max_harmonics = [50, 23, 7, 4, 3, 2, 1]
harmonics = list(map(lambda x: x * 2 + 1.0, max_harmonics))
分母の側、\(\frac{1}{\sin(\pi\phi)}\)を見てみます。
# denominator part of SincM
plt.plot(t, 1. / np.sin(np.pi * t), color=colors[0], linewidth=1.0)
plt.xlabel('t')
plt.ylabel("$1 / \sin(x)$", fontsize=16)
plt.xlim(min_phi, max_phi)
plt.xticks([0.5, 1, 1.5, 2, 2.5],["0.5$\phi$", "$\phi$", "1.5$\phi$", "2$\phi$", "2.5$\phi$"])
plt.ylim(-10, 10)
plt.grid(True)
plt.show()
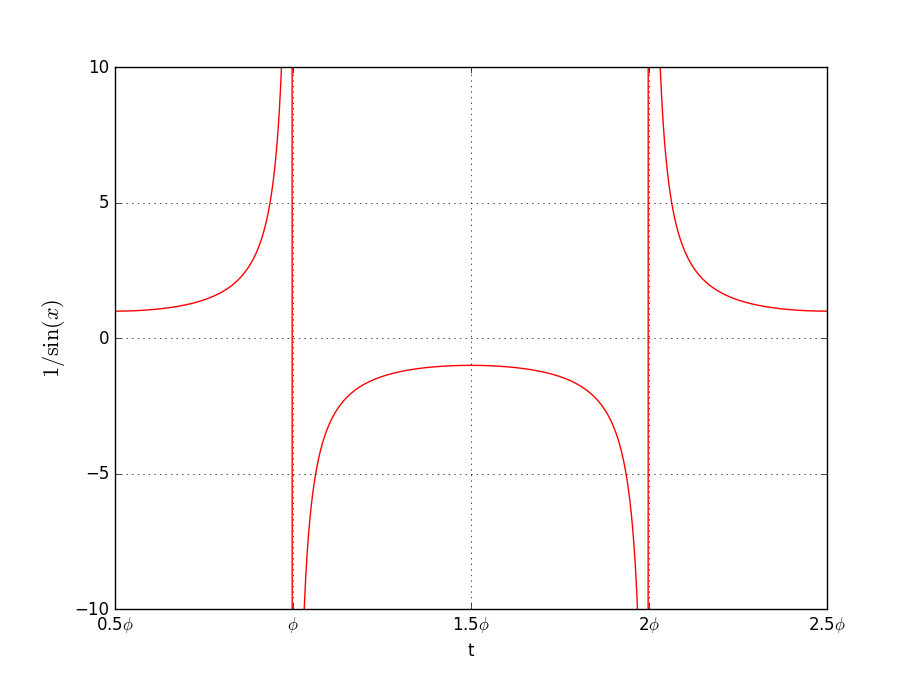
\(\frac{1}{\sin(\pi\phi)}\)はこんな感じです。
サイン関数は0と\(\pi\)のとき値が0になるので、その逆数は無限大になります。
分子の側\(\sin(M\pi \phi)\)はただのサイン関数ですが、上と並べて見てみましょう。
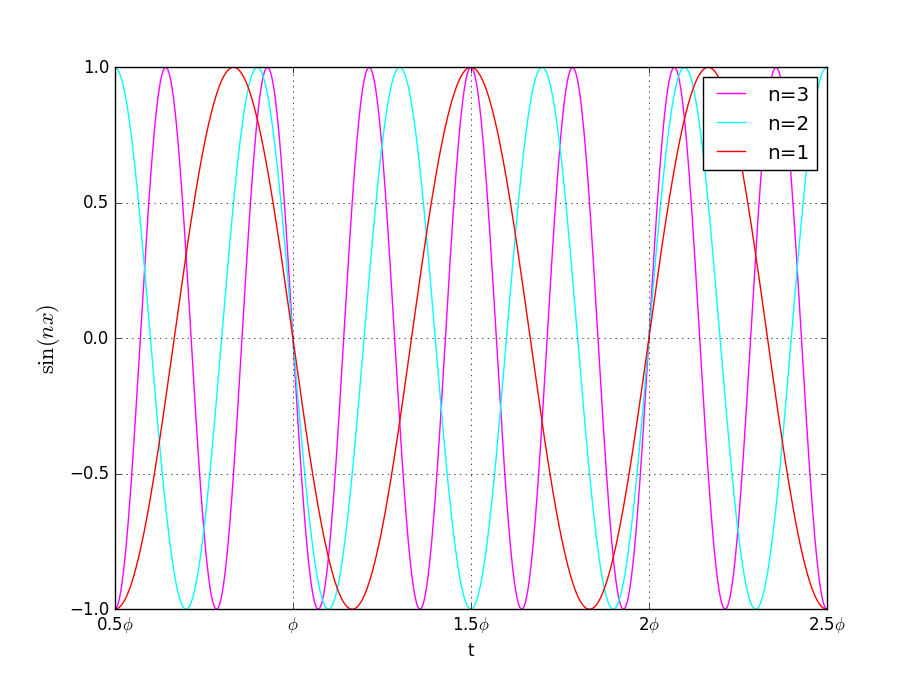
\(\phi\)および\(2\phi\)のところで、分母、分子が必ずゼロになることが見て取れます。
鋸波の波形が不連続に変化するのは、この部分です。
\(Sinc_M\)という関数は、上の波形と下の波形を掛け算するということですが、こんな波形になります。
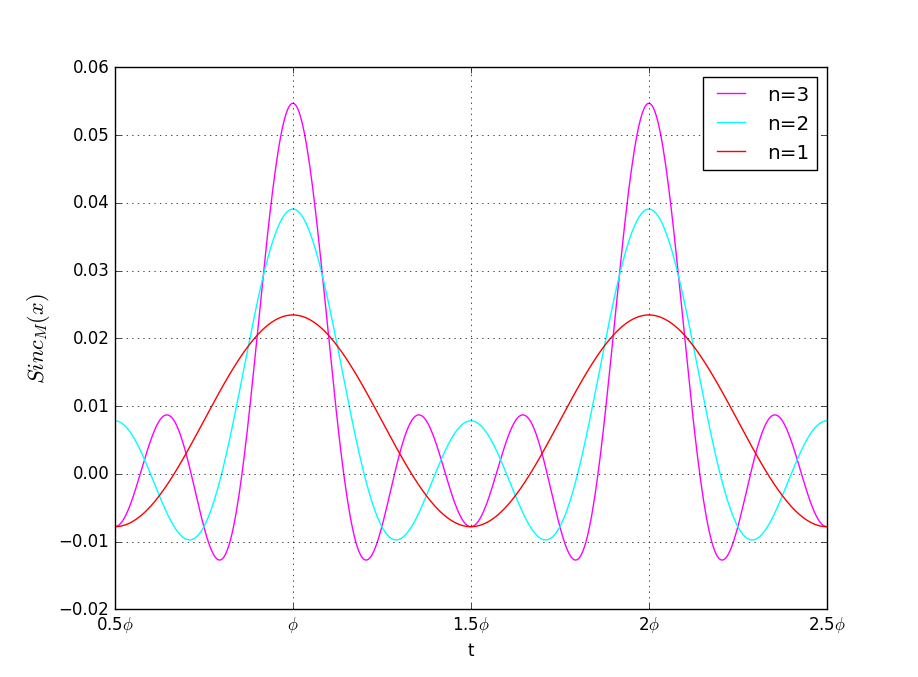
# generate SincM wavetables
wave_tables = []
period = table_size / (max_phi - min_phi) / 2
for h in harmonics:
wt = np.zeros(shape = (t.shape[0],),)
wt += np.sin(np.pi * h * t) / np.sin(np.pi * t) / period
wave_tables.append(wt)
# SincM
for i in range(4, len(wave_tables)):
plt.plot(t, wave_tables[i], color=colors[i % 6], linewidth=1.0, label='n='+str(max_harmonics[i]))
plt.legend()
plt.xlabel('t')
plt.ylabel('$Sinc_{M}(x)$', fontsize=16)
plt.xlim(min_phi, max_phi)
plt.xticks([0.5, 1, 1.5, 2, 2.5],["0.5$\phi$", "$\phi$", "1.5$\phi$", "2$\phi$", "2.5$\phi$"])
plt.grid(True)
plt.show()
\(M\)を大きくしていくと、ピークがより先鋭になっていきます。
そのままグラフを描くと、\(M\)が大きいときのY軸の値が大きくなって比較しにくいので、ピークの高さが一致するように正規化したものが下図です。
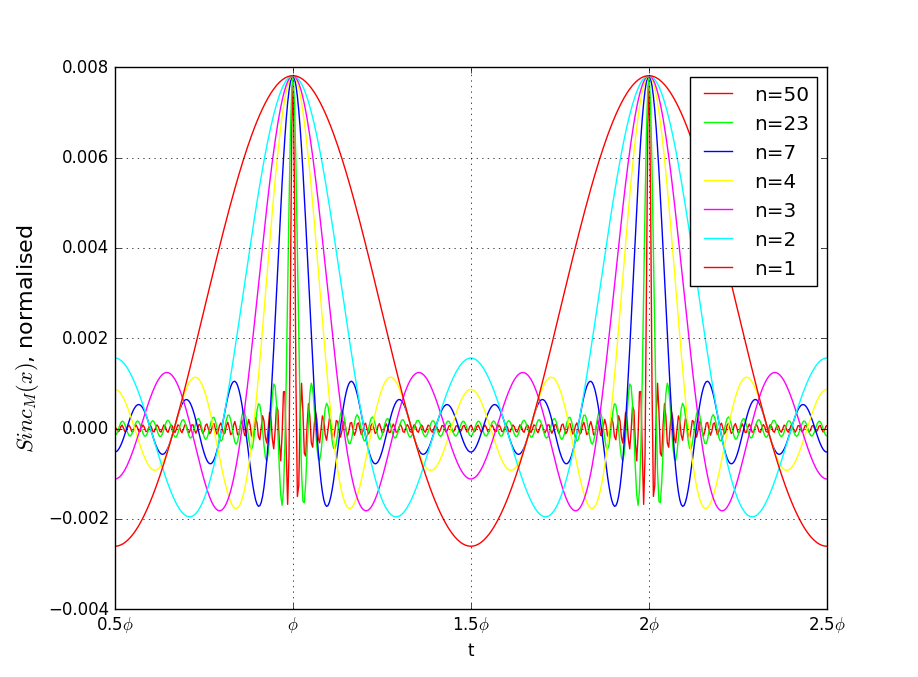
Bandlimited Impulse Train、「帯域制限されたインパルス列」の姿が見えてきましたね。
次に、これを時間軸で積分します。
# Integrated SincM
for i in range(0, len(wave_tables)):
plt.plot(t, np.cumsum(wave_tables[i]), color=colors[i % 6], linewidth=1.0, label='n='+str(max_harmonics[i]))
plt.legend(loc="lower right")
plt.xlabel('t')
plt.ylabel('$\int Sinc_{M}(x)$', fontsize=16)
plt.xlim(min_phi, max_phi)
plt.xticks([0.5, 1, 1.5, 2, 2.5],["0.5$\phi$", "$\phi$", "1.5$\phi$", "2$\phi$", "2.5$\phi$"])
plt.grid(True)
plt.show()
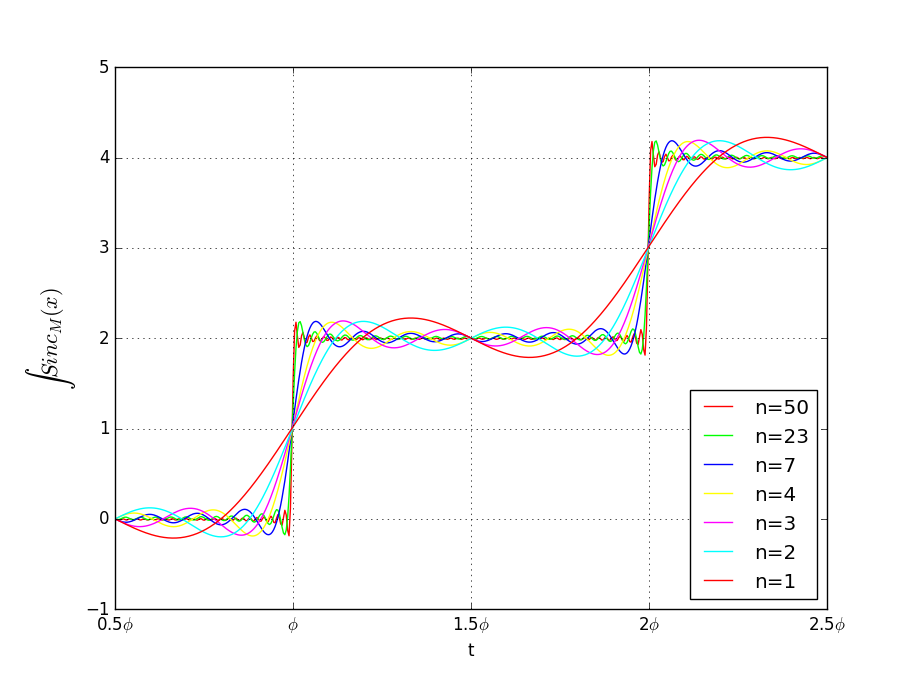
すると、このような階段状の波形ができます。鋸波まであと一息です。
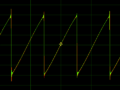
水平になっている部分が右下がりになるように、かつ波長1つぶんでちょうど1.0から-1.0まで下がるように、引き算してやります。
# Integrated (SincM - constant)
average = 1. / period
for i in range(0, len(wave_tables)):
plt.plot(t, np.cumsum(wave_tables[i] - average), color=colors[i % 6], linewidth=1.0, label='n='+str(max_harmonics[i]))
plt.legend(loc="lower right")
plt.xlabel('t')
plt.ylabel('$\int Sinc_m(x) - kx$', fontsize=16)
plt.xlim(min_phi, max_phi)
plt.xticks([0.5, 1, 1.5, 2, 2.5],["0.5$\phi$", "$\phi$", "1.5$\phi$", "2$\phi$", "2.5$\phi$"])
plt.ylim(-1.2, 1.2)
plt.grid(True)
plt.show()
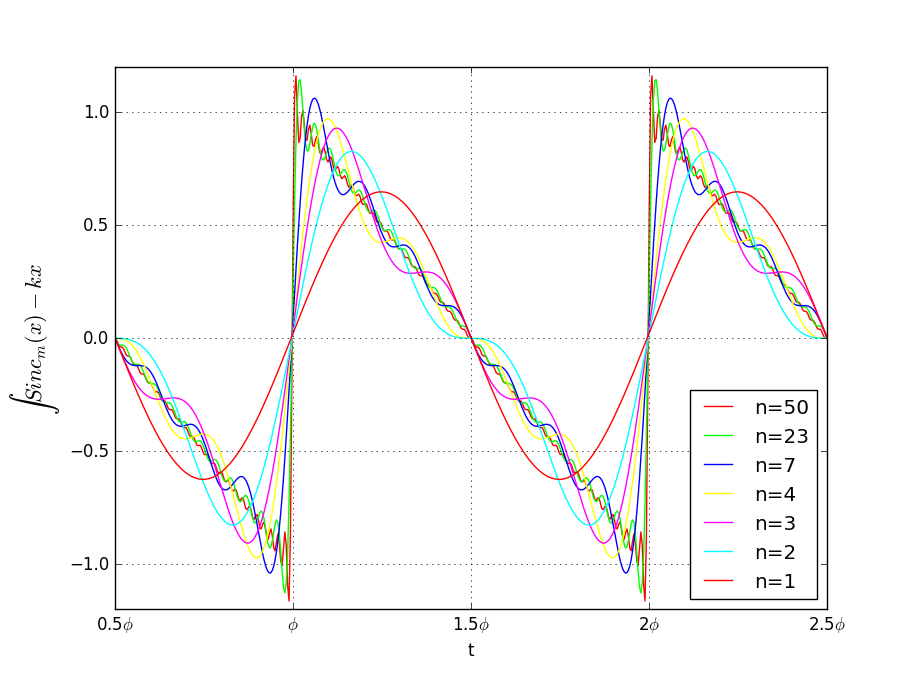
おお、ちゃんと鋸波ができました!
最初に挙げた、フーリエ級数で作成した波形と同じものができています。
次回は、これをlogue SDK上でオシレータとして実装します。

コメント