以前、こちらの記事で
「エンベロープに関しては根が深いので、別の記事で書こうと思います。」
と書いたのですが、結局まだ記事を書いていませんでした。今回はこのエンベロープの話です。
調べてみたらg200kgさんが既にいくつか記事を書かれていて、二番煎じになるかもしれませんが・・・

さて、シンセサイザでポピュラーなのはADSR型のエンベロープですが、まずはよりシンプルなAttack-Decay型のエンベロープから始めます。
トリガ信号(短いパルス)を受けると、だんだん出力電圧が高くなり(Attackフェーズ)、一定の値に到達すると今度はだんだん電圧が低くなっていきます(Decayフェーズ)。
ハードウェアでの実装は、コンデンサを充電したり放電したりで実現するのがポピュラーです。
以下はタイマーIC555を使った例です。
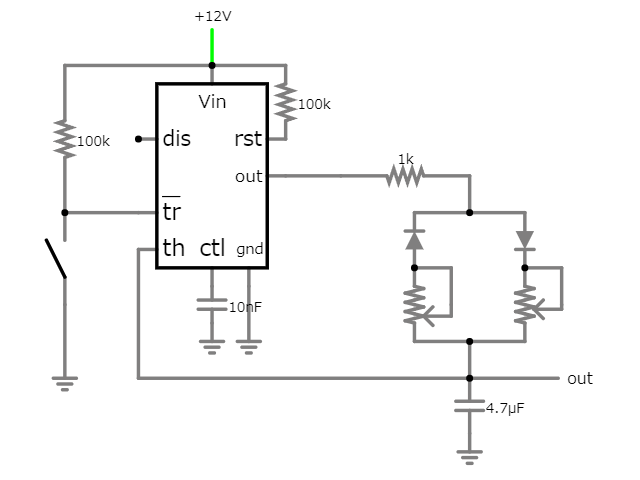
555は単安定モードで動いており、左下のスイッチをチョット押してトリガ信号を与えると、555の出力がHとなって右側のダイオードを通って右下のコンデンサを充電します。
コンデンサが充電されて、555のスレッシュホルド(VCCの2/3)に到達すると、555の出力はLに戻り、コンデンサは左側のダイオードを通じて放電されます。
以下はcircuitjsでのシミュレーションです。
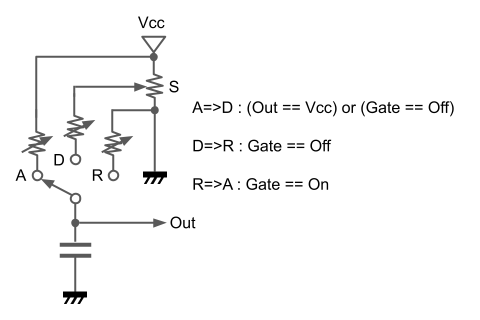
ADSR型エンベロープの回路は検索するといろいろ出てきますが(これなど解りやすいかも)、要はDecayフェーズを2つに分けます。
1つ目のDecayフェーズはコンデンサを放電する電圧を0VではなくSustainレベルの電圧とします。
2つ目のDecayフェーズはゲート信号がOFFになるとトリガされ、コンデンサを0Vまで放電させます。
ものすごく模式的に書くと下図のような感じです。
それで、ようやくソフトウェアでの実装の話になりますが、これをよくあるこの図を頭に置いて実装すると、変な実装になることがあるんですね。
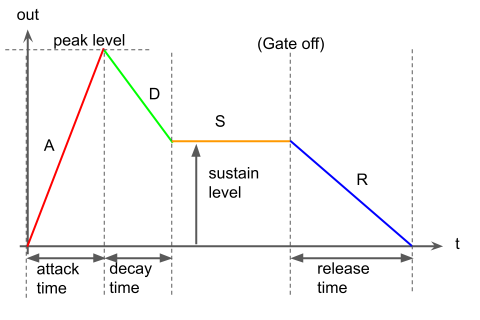
ADSRそれぞれのフェーズを「線分」として見てしまうと、それぞれのフェーズに「始点(x0, y0)」「終点(x1, y1)」があって、その間を線で結ぶ、というように考えてしまいます。
この記事を書くきっかけになったMaximilianのmaxiEnvGenクラスの実装が、まさにそういったモデルになっています。
ですが、このようなモデルだと「Attackフェーズの途中でGate OffとなりReleaseフェーズへ移行」みたいなパターンがうまく表現できません。Releaseフェーズの始点はSustainレベル、と固定されているとおかしなことになります。
上述の回路を考えると、実際には「コンデンサに溜まっている電荷=現在のyの値」と、現在のフェーズによって定まる充・放電ペースが基本的なパラメータです。これらをうまく表現するためには「始点」「終点」という絶対値ではなく、「傾き」というベクトルに着目する必要があります。
このmaxiEnvGenクラスの実装を直してあげられないかなと思ったのですが、根本にあるモデル自体を取り替えないといけないので難しそうでした。
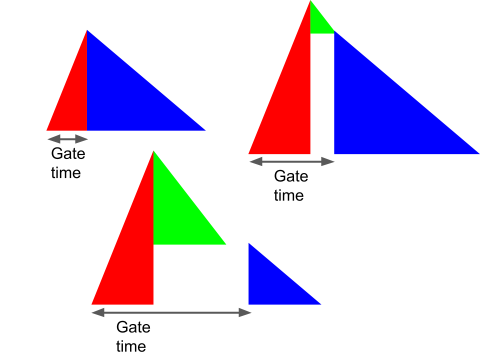
図形的なアナロジーで考えるなら、下図のように直角三角形のモデルで考える方が(より「傾き」を直観的に扱えるという意味で)少しましなのではと思います。
それぞれの直角三角形の縦横比(=斜辺の傾き具合)は、縦の値は固定とし、Attackタイム、Decayタイム、Releaseタイムだけで決めます。
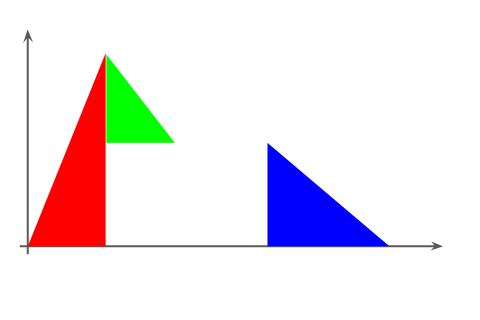
例えばAttackフェーズの三角形は、幅がAttackタイム、高さがPeak Level(固定)という縦横比になります。
実際のエンベロープ信号はこれらの三角形の組み合わせで、それぞれの三角形は縦横比を変えない前提で自由に拡大縮小してよく、ただし制約として
・斜辺同士がスムーズに接続されなければならない(ただしSustain区間で水平方向に離れるのは許容)
・Attackフェーズの高さはPeak Levelを超えてはいけない
・Decayフェーズの高さは(PeakLevel – SustainLevel)を超えてはいけない
・Decayフェーズは、Attackフェーズの高さがPeak Levelのときしか使えない
という条件があると考えます。
すると、たとえば下図のような組み合わせができることが分かります。
あとエンベロープのカーブについて付け加えると、アナログ回路の場合は上の図のような直線にはなりません。
上に挙げた555を使った回路で言うと、エンベロープ出力は555の出力信号の矩形波をRCローパスフィルタを通したものになっています。
そのカーブは
$$V(t) = Vmax(1 – \exp(\frac{-t}{τ}))$$
となります。\(τ\)は傾きを決めるパラメータです。
ちなみに先日移植したBraidsはAD型のエンベロープを持っていますが、実装としてはエンベロープの値はテーブルを参照しており、そのテーブルは\(t=[0, 1.0]\)の区間で
$$E(t) = 1 – \exp(-4t)$$
で生成していました。このテーブルのインデックス値は、実際のAttack/Decayタイムの設定値に応じてスケーリングされます。テーブルの値についても、フェーズ開始時点のエンヴェロープの値・フェーズ終了時点の目標値(最大値または0)でスケーリングされます。
(drumlogue移植版ではエンベロープカーブをこのテーブルの値とリニアの値の範囲で可変としています。)

コメント