RaspberryPi PicoのInterpolatorで疑似3Dのカーレース風デモを作ってみた

今回はPicoで作ったこのデモの紹介をします。

I made @Raspberry_Pi Pico interpolator SNES mode7 style demo using @pimoroni Display pack. Yay! pic.twitter.com/0DBXAKcruL

— boochowp (@boochowp) February 23, 2021

擬似3Dで奥行きを表現していますが、これは基本的には以前作ったテクスチャマッピングの応用です。記事内で紹介した、RP2040のデータシートに記載されている「スーパーファミコンのMODE7のような処理」に相当します。

以前作ったテクスチャマッピングのデモでは、テクスチャの拡大・縮小を行っていますが、この拡大縮小の比率を、「画面上に行くほど小さく、画面下に行くほど大きく」なるようにしてやれば、奥行き感が出せます。（横方向だけでなく縦方向にも拡大縮小が必要です。）

testing @Raspberry_Pi Pico hardware interpolator as a texture mapper pic.twitter.com/ZsuTwTVrtO

— boochowp (@boochowp) February 9, 2021

また、このときは16×16ピクセルのテクスチャを使いましたが、今回は4096×8192ピクセルの画像を使っています。このような大きな画像はそのままではメモリに入り切りませんので、何種類かの16×16ピクセルの画像を用意し、それらを256×512個並べています。

以下の説明では、16×16ピクセルの画像を「タイル」、タイルを256×512個並べたものを「マップ」と呼びます。

というわけで、以下、中身の解説です。
今回のコードは以下にアップロードしてあります。

https://github.com/boochow/pico_test_projects/tree/main/interpolator2

まず疑似3Dの処理ですが、これ自体は既によく知られている手法ですので、ご存じの方は読み飛ばしていただいて構いません。雰囲気だけ知りたい方は、以下の動画が面白いと思います。（双曲線の導入が天下り的ではありますが。）

これ以降の解説では、下の図のような座標系を使います。スクリーンはXY平面、マップは UV 平面上にあります。スクリーンの手前にカメラ（視点）があり、スクリーンを通してマップ上の点を見ています。

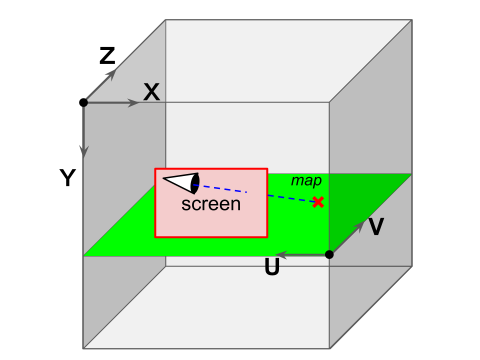
なお、UV平面とXZ座標平面は平行ですが、UとXは逆向きです。なぜこうしたかというと、マップは画像なので、左上を原点として右と下を正方向としたほうが実際の画像データを扱うには都合が良いからです。

やりたいことは、カメラの位置とスクリーン上の座標から、マップ上の点の座標を求め、その色を調べることです。カメラとスクリーンとの位置関係は固定とします。

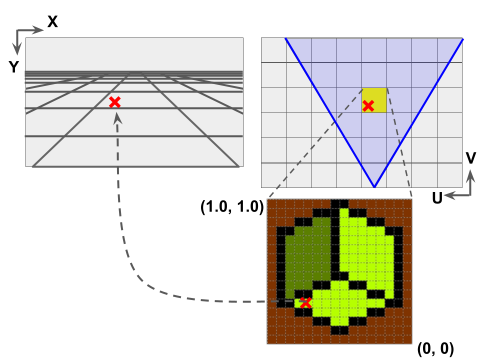
上の図は左がスクリーン上の画像、右上がマップを上から見たところです。スクリーンに映っているのは、2本の青線で囲まれた V 字型の領域です。

マップ上のマスの一つ一つがタイル一個を表しています。 UV座標系でのタイルの大きさは、1×1とします。従って、マップ上の点の座標(u, v)が求まった時、座標の整数部がマップ内でのタイルの位置を表します。

まず、vの値を求めてみましょう。
下の図はYZ平面の図です。視点がOにあり、スクリーンはZ方向に視点からdだけ離れています。また、マップはY方向に視点からzだけ離れています。

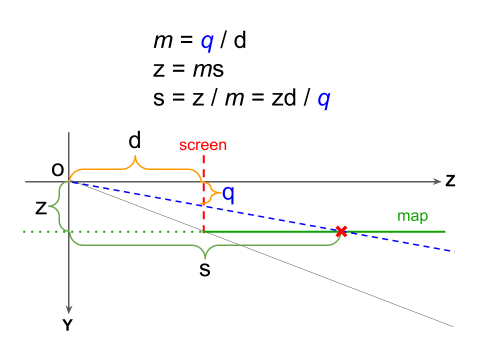
スクリーン上のピクセルのY座標がqだとすると、視線からピクセルに向かう直線の傾きはq/dですので、この直線がマップと交差する点のZ座標は

s = zd / q

と求めることができます。スクリーンに描画している間、qは変化しますがzもdも変化しませんので、sとqの関係はグラフとしてはf(x)=c / xという関数のグラフと同じになります。

一方、uの値は、ピクセルのX座標がpだとすると、上のsの値を使って

-t = sp / d = zp / q

と求まります。tではなく-tとなっているのは、U軸がX軸と逆方向だからです。

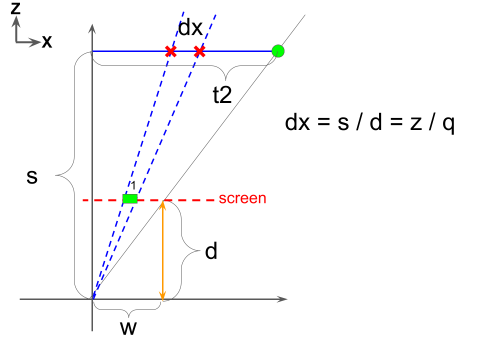
スクリーンの横幅が2wピクセルだとすると、スクリーンの右端のピクセルに相当するマップ上の点のx座標は

-t2 = zw / q

となります。また、スクリーン上で隣り合うピクセルの間で、uの値が変化する度合いdxは

-dx = s / d = z / q

となります。

整理しますと、

視点からスクリーンまでの距離：d
視点からマップまでの距離：z

のとき、

スクリーン上の座標(p, q)に対応するマップ上の座標： (zd / q, zp / q)
スクリーン上で隣り合うピクセルの、マップ上での距離：z / q

となります。

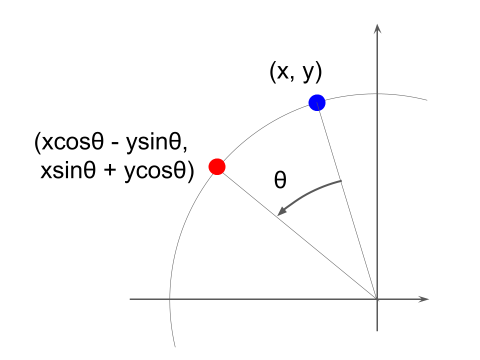
疑似3D変換の基本的な演算は以上です。詳細は省きますがこの他、視点の移動や左右方向の回転を考慮して座標変換する必要があります。回転の演算は、以下の図のように座標(x, y)を

(xcosθ – ysinθ, xsinθ + ycosθ)

に移します。

※※※

次に、Interpolatorを使った描画処理です。テクスチャマップと同じ処理を２つ用い、１つをタイルの特定、１つを色の特定に使用します。

上に述べた計算で、スクリーンの座標 (p, q) に対するマップ上の点 (s, t) が得られました。マップのサイズは1×1ですので、(s, t)の整数部だけを取り出すとマップの位置が得られます。一方、小数部だけを取り出すと、タイルの中での描画したいピクセルの位置が分かります。

sとtは、それぞれ整数部16ビット、小数部16ビットの固定小数点数とします。マップが256×512、タイルが16×16ピクセルとすると、sは整数部8ビット・小数部4ビット、tは整数部9ビット・小数部4ビットで表現できます。

Interpolatorを使うと、下図のように座標の加算を行って整数部（あるいは小数部）だけを取り出し、マップデータやタイル画像データの先頭からのオフセット値を算出して出力することができます。

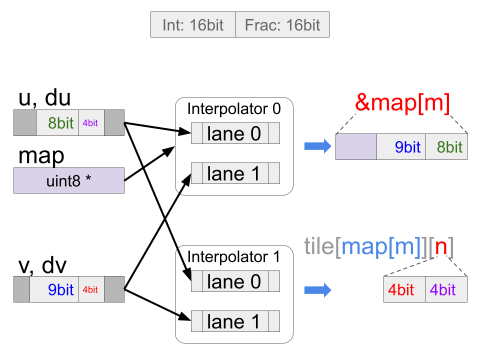
この処理をさせるためのInterpolatorの設定は、下図のようになります。内容はテクスチャマッピングと全く同じで、与えている数値が異なるだけなので、説明は割愛します。

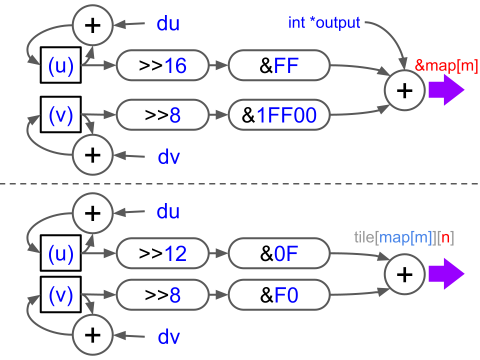
テクスチャマッピングのデモと疑似3Dとの描画処理の違いは、疑似3Dでは横一列ぶんのピクセルごとにInterpolatorに与えるパラメータを再計算することです。これは、スクリーン上のY座標が変わると、付随して疑似3Dで用いる拡大・縮小の比率が変わるためです。

※※※

Interpolatorを使って、短いコードでMODE7のエミュレーションができました。Interpolatorは最初はちょっと敷居が高いかもしれませんが、活用するといろいろ面白いことができそうです。

また今回、Picoがフラッシュを外付けで2MBも載せたのは英断だなと思いました。これくらいあればSDカードなしでもそこそこデータを格納できますので、今回のようなデモを作るには都合が良いです。今回のマップは256×512=130KBなのでSRAMにも格納できますが、これが1024×1024だったら1MBですから、フラッシュでなければ入りきりません。（GitHubにはPNGファイルからマップを生成するスクリプトも入れてありますので、オリジナルのマップを作ってみたい方は試してみてください。）

なお今回のデモはTom’s hardware guideのニュースで紹介されました。PCパーツのレビューのサイトというイメージだったのですが、マイコンも扱うんですね。