前回紹介したレイトレーシングの手法は、時間がかかりすぎるのでゲームの画像表示に使うには向いていません。
今回は、球を一つだけ、レイトレーシングよりも高速に描画するプログラムを作ってみます。
上の画面が実行結果で、直径170ピクセルの球を0.6秒弱で描画しています。
アニメーションに使うのは難しいですが、スプライトやBGの作成には使うことができるでしょう。
球を球らしく見せるには、陰影が重要です。
光の方向や強さなどに応じてピクセルの明るさを決めることを「シェーディング」と言います。
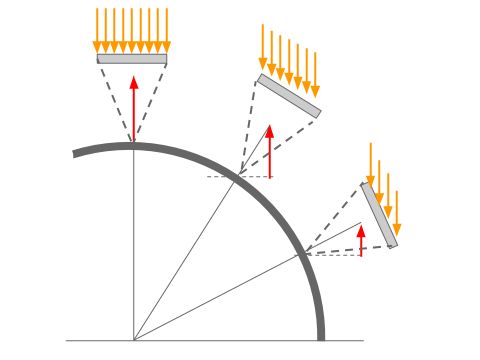
下図は球面が上方から来る光に照らされている様子を示しています。
(以下、球面の光の当たらない下半分は無視します。)
地球が太陽に照らされている様子を思い浮かべれば分かりやすいでしょう。
このときシェーディングは基本的には以下のようにして行えます。
まず、球面のごく小さな一部を考えます。
これは、ある傾きを持った平面にほぼ等しいと考えられます。
この小さな平面の明るさは、光が来る方向(図では垂直方向)に対して平面が直角(図では水平)になっているとき、最大になります。
平面が傾くにつれて暗くなっていき、面が垂直になったときに明るさはゼロになります。
この明るさは、ある長さの棒を平面に対して垂直に立てるとき、その棒の両端の座標のZ値の差分(図の赤い矢印)に比例します。
プログラムにするために、上記を数式に直してみます。
図では上から光が来ていますが、この上方向をZ軸とします。
そして、球面の中心を原点とします。
球面上の点は、半径をrとすると
x2+y2+z2=r2
を満たします。
このとき、シェーディングに必要な値である赤い矢印の長さは、実は球の半径とzの値だけで決まります。
直感的にはちょっとわかりにくいかもしれませんが、zが最大となるのは図の球面の一番高い部分(中央部分)で、このときx=y=0でz=rとなり、図の球面の両端部分ではz=0となるのはすぐわかると思います。
球面に垂直に棒を立てると、その棒は必ず球の中心を指します。
従って
・棒を斜辺とし、水平および垂直な辺を持つ直角三角形
・球面の中心から棒を立てた点までの線分を斜辺とし、水平および垂直な辺を持つ直角三角形
は相似の関係になります。
すると、
・棒の長さと、赤い矢印の長さの比
・球面の半径と、棒を立てた点のZ座標値の比
が等しいことが言えるので、棒の長さが1のとき、赤い矢印の長さは(棒を立てた点のZ座標値/球面の半径)となります。
以上を用いて、球を光源側から見た場合(図では上方向から見た場合)の画像を描いてみます。
先に書いたとおり、球面の方程式は
x2+y2+z2=r2
です。
従って半径rの球面を描くには、x,yを変化させて、それに対応するzの値を
z=SQR(r2-x2-y2)
で求め、zの値に応じて(x,y)のピクセルの明るさを変化させます。
プログラムは以下のようになります。
CLS:GCLS T=MAINCNT DRAWSPHERE 100,20,170,255,255,176,0.2 PRINT (MAINCNT-T)/60;" SECONDS ELAPSED" DEF DRAWSPHERE X0,Y0,SIZE,R0,G0,B0,GL VAR R,RR,X,XX,Y,YY,Z,ZZ,YMAX,NZ,NY,C,R1,G1,B1 R=SIZE/2+0.5 RR=R*R X0=X0+R Y0=Y0+R X=-0.08 WHILE R>=X Y=X XX=X*X YY=XX YMAX=RR-XX ZZ=YMAX-YY WHILE ZZ > 0 Z=SQR(ZZ) NZ=Z/R C=SHADING(NZ,1-GL,GL) RGB_ADD 0,0,0,C,R0,G0,B0 OUT R1,G1,B1 C=RGB2(255,R1,G1,B1) GPSET X0+X,Y0+Y,C GPSET X0-X,Y0+Y,C GPSET X0+X,Y0-Y,C GPSET X0-X,Y0-Y,C GPSET X0+Y,Y0+X,C GPSET X0-Y,Y0+X,C GPSET X0+Y,Y0-X,C GPSET X0-Y,Y0-X,C Y=Y+1 YY=Y*Y ZZ=YMAX-YY WEND X=X+1 WEND END DEF SHADING(VAL,DIF,AMB) RETURN AMB+DIF*VAL END DEF RGB_ADD R0,G0,B0,K,R1,G1,B1 OUT R2,G2,B2 R2=MIN(255,R0+K*R1) G2=MIN(255,G0+K*G1) B2=MIN(255,B0+K*B1) END DEF RGB2(A,R,G,B) IF RND(8) < (R AND 7) THEN R=R+8 IF RND(8) < (G AND 7) THEN G=G+8 IF RND(8) < (B AND 7) THEN B=B+8 RETURN RGB(A,R,G,B) END
手続きDRAWSPHEREが描画処理の本体です。
パラメータは
・左端のX座標
・上端のY座標
・直径
・色(R,G,B)
・環境光係数
となっています。
球のサイズは半径ではなく直径で指定しています。
球は一辺が直径に等しい正方形の領域に描画されます。
最後のパラメータ「環境光係数」には、通常0.1~0.2程度を指定します。
このパラメータは球全体の明るさを底上げします。
1.0を指定すると、陰影のない塗りつぶした円が描画されます。
DRAWSPHEREの中身は2重のループになっています。
外側のループがX座標を1ずつ増やし、内側のループがY座標を1ずつ増やします。
(X0,Y0)が中心の座標です。
内側のループの中で、GPSETを8回連続して行っています。
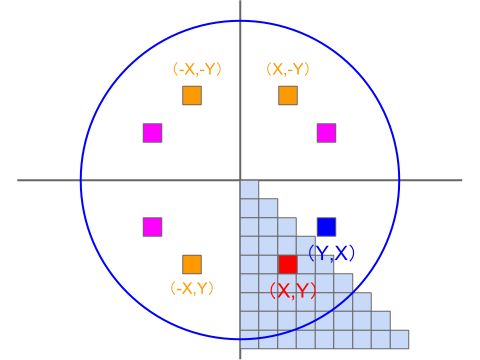
今回描画する球では、明るさの値は原点を中心とした同心円上で同じ値になります。
従って下図のように、座標を入れ替えたり符号を反転することによって、一度の計算で8か所のピクセルの値が決まります。
全体の1/8を計算すれば十分なので、ループは図の網掛けした部分だけをカバーしています。
RGB_ADD手続きは、その名の通り色の加算(と定数倍)を行う手続きです。
色(R0,G0,B0)に色(R1,G1,B1)をK倍したものを加算し、結果を(R2,G2,B2)に代入します。
RGB2関数は前回も説明しましたが、疑似的に中間色を生成して色の変化を滑らかに見せます。
なお、ピクセルが球の内部か外部かを判定する際、境界値付近での判定を意図的に制御するために、変数の初期値等を小数点以下のオーダーで幾何学的な値よりも大きくしたり小さくしたりしています。
たとえば
・半径Rが直径の1/2よりも0.5大きい
・Xの初期値が0ではなく-0.08
などです。
いずれも幾何学的には、0.5や-0.1は不要ですが、特に径が小さい円を描くとき、形状に微妙な違いが出てきます。
掲載したプログラムは、直径が16ピクセルや14ピクセルの形状が私の好みのもの(下図)になるように調整しています。
(その代わり、直径15ピクセルを指定しても16ピクセルになってしまいますが・・・)
今回のプログラムは、球を正面から光で照らした場合の陰影を計算しています。
ちょうど、満月のようなものです。
次回はこのプログラムを少し拡張して、前回のレイトレーシングの例で示したような、斜め方向から照らした場合の陰影を計算してみます。





コメント
なんか、WENDが足りないWHILEがあるって表示されるのですがどうすれば良いですか?
う~ん、下から1/3あたりのところにある
ZZ=YMAX-YY
WEND
X=X+1
WEND
END
このへんの入力ミスではないでしょうか?
出来ました、ありがとうございました。
もうひとつ、質問です。
RGB_ADD 0,0,0,C,R0,G0,B0 OUT R1,G1,B1のところで、エラーが出ます、どうすれば良いですか?
言わなくても、分かると思いますが、プチコン3号初心者です。
うーん、どんなエラーでしょう?
また、最後のほうの
DEF RGB_ADD R0,G0,B0,K,R1,G1,B1 OUT R2,G2,B2
R2=MIN(255,R0+K*R1)
G2=MIN(255,G0+K*G1)
B2=MIN(255,B0+K*B1)
END
これは正しく入力されているでしょうか?
打ち忘れてましたので、打ってきたところ、入力したDEF命令にシステムエラーが出ました…
どんなエラーでしょう?
また、変数名(特にR2, G2, B2)の入力ミスはありませんか?