ゴールデンウイークということで、あまり人気のない(?)波形生成の話をしてみます。
鋸波や矩形波などの波形をデジタルで生成しようとすると、エイリアスノイズの問題が発生します。鋸波や矩形波には、無限に高次のの倍音成分が含まれており、これらはDAコンバータで出力することができないためです。出力できなかった倍音成分は、折り返されて低い周波数のノイズとなって出力されてしまいます。
これを防ぐためには、ナイキスト周波数よりも高い周波数の倍音成分を含まない鋸波や矩形波を生成する必要があり、そのための方法として、
以前、BLIT(Band-limited Impulse train)を紹介しました。
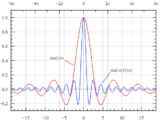
BLITでは、生成したい波形の導関数をまず計算し、それを積分して所望の波形を生成していました。
今回紹介するBLEPは、これとはまったく逆のアプローチです。
BLEPとはBand-Limited stEP functionの略だそうで、「ステップ」とは、鋸波や矩形波において不連続にジャンプしている部分を指しているようです。
下の図は、何も考えずに鋸波を実装した場合のグラフです。
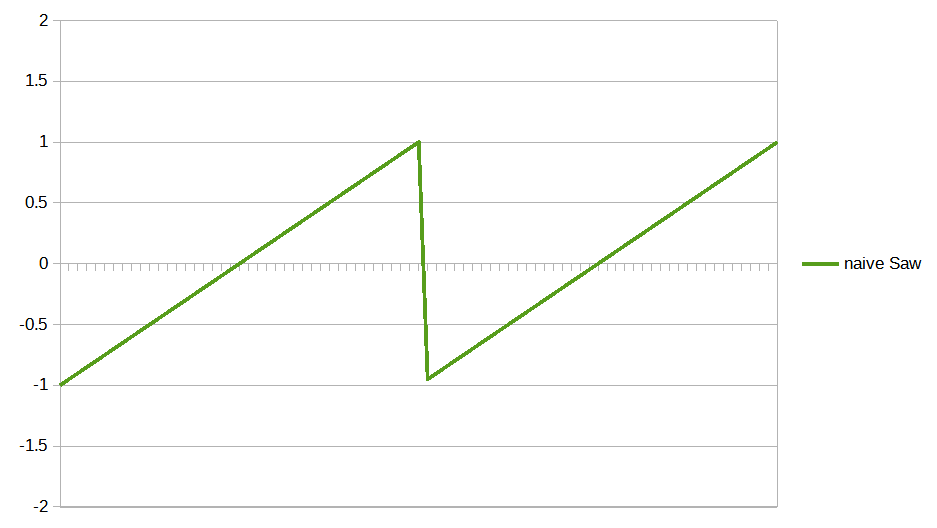
数式で書くとこうなります。
$$y(t) = 2t – 1 (ただし 0 \le t \lt 1)$$
これは\(t = 0\)のところで、階段状の不連続な変化が起こるので、エイリアスノイズの原因になります。
BLEPの基本的な考え方は、この階段状の変化の部分をなだらかにしてやれば、ノイズを減らせるだろうということです。
下の図で赤で示しているのが、なだらかにした波形で、点線が元の波形(緑)との差分です。
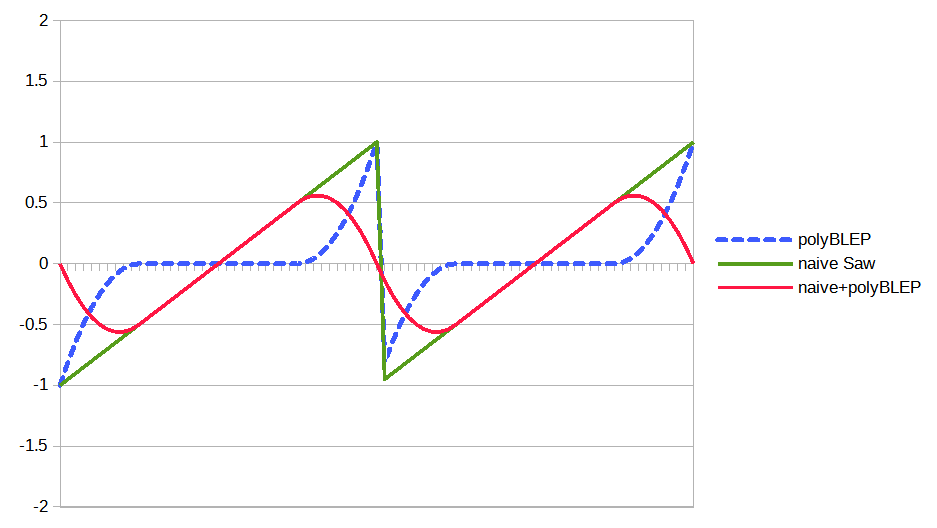
「まず緑の波形を作って、そこから点線の波形を減算して、赤の波形を生成する」というのがBLEPのコンセプトです。
この点線(差分)の波形ですが、ナイキスト周波数のサイン波と、\(y(t)=0\)の合成で作れそうな雰囲気ですね。
しかし、PolyBLEPではこの波形を二次関数で近似しています。Polyはpolynomial(多項式)から来ています。多項式を使ったBLEP関数ということです。
以下のスレッドに、PolyBLEPの実装例があります。

引用すると以下の通りです。
double t = 0.; // 0 <= t < 1
double dt = freq / sample_rate;
...
double poly_blep(double t, double dt)
{
// 0 <= t < 1
if (t < dt)
{
t /= dt;
// 2 * (t - t^2/2 - 0.5)
return t+t - t*t - 1.;
}
// -1 < t < 0
else if (t > 1. - dt)
{
t = (t - 1.) / dt;
// 2 * (t^2/2 + t + 0.5)
return t*t + t+t + 1.;
}
// 0 otherwise
else
{
return 0.;
}
}このコードで書かれている式をグラフにすると、下図のようになります。
これは、生成する鋸波の周波数がナイキスト周波数の\(1/2\)のときのイメージです。
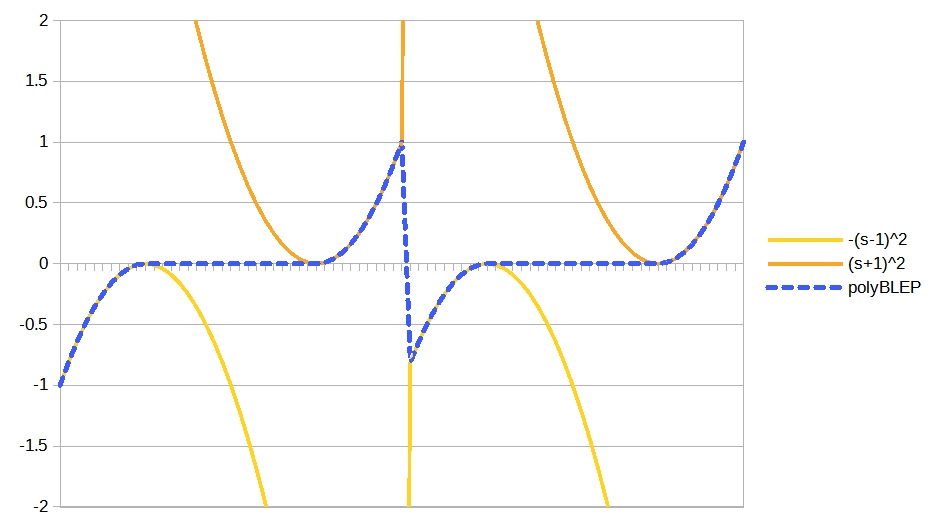
左端を\(t=0\)、中央の不連続部分を\(t=1\)とすると、
\[ y(t) = \begin{cases}
0 \le t \lt 0.25 & 負の側の二次曲線 \\
0.25 \le t \lt 0.75 & 0 \\
0.75 \le t \lt 1 & 正の側の二次曲線
\end{cases}
\]
となっています。
ふたつの二次曲線は、\(f_s\)をサンプリング周波数、\(dt = f / f_s\)、\( s = t / dt \)と置いた時の
$$y = -(s-1)^2 \\
y = (s+1)^2 $$
という関数になります。
最後に、以上の3つをグラフ上で重ね合わせると以下のようになります。
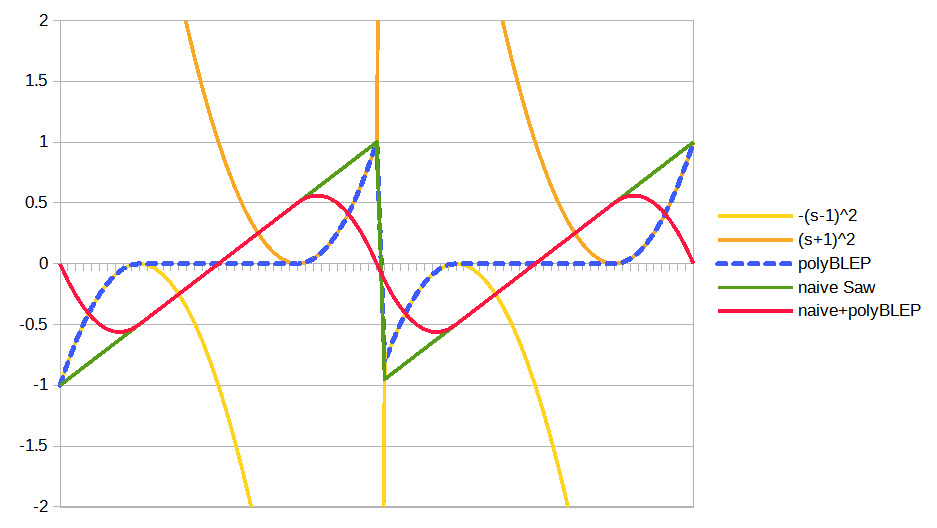
なお、上の式に現れる\(tとdt\)は、logue SDKでいうところのphaseとw0に相当します。phaseはw0ずつ増えていきますので、実際の波形生成の途中で上の関数が0以外の値を持つのは、波形が不連続な変化をする前後の1サンプルずつということになります。
PolyBLEPは、三角関数を二次曲線で近似したり、不連続な部分以外を無視したりと、やや荒っぽい手法ではあるのですが、確かにエイリアスノイズは気にならない程度に抑制できます。
BLITと関連付けて考えるなら、BLITでは元波形を微分したときの不連続に変化している箇所(インパルス)をSinc関数で表現していましたが、PolyBLEPでは傾きが正と負の2つの一次関数で作った山型の関数で近似していることになります。
しかし実装上は、BLEPは1次関数を積分するのではなく2次関数を直接計算しますので、BLITのような積分の処理が入りません。
その結果、出力が安定しますし、計算量も非常に軽くなります。
大きなウエーブテーブルを乗せることができないマイコンでの波形生成には、有効な方法と思われます。
なお、BLEPについては以下の記事が参考になります。

C++による実装が以下のリポジトリにあります。

コメント