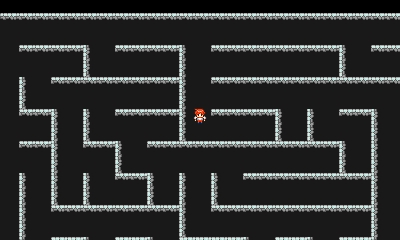
前回、BGに迷路を表示させることができましたので、今度はプレイヤーのキャラクタを中央に置いて迷路の中を歩き回れるようにします。
ドラゴンクエストで、ダンジョンの中を歩き回るときのような感じです。
前回、迷路を表示してスクロールすることはできていますので、今回と前回の表示の違いは、画面中央にプレイヤーキャラがあるかどうかだけです。
しかし実際には、
・迷路の中で実際にプレイヤーキャラを動かしてみて
・壁にぶつかった場合は壁の手前までの移動に修正し
・プレイヤーキャラの新しい位置に応じて迷路をスクロール
という処理が必要になります。
壁に衝突したかどうかの判定のために、まず迷路のマップを表すデータを作ります。
BG表示のときは、迷路の各部屋を2×2の絵で表現しましたが、マップデータでは壁と通路をより明確に分離するために、迷路の1部屋を4×4のマス目で表すことにします。
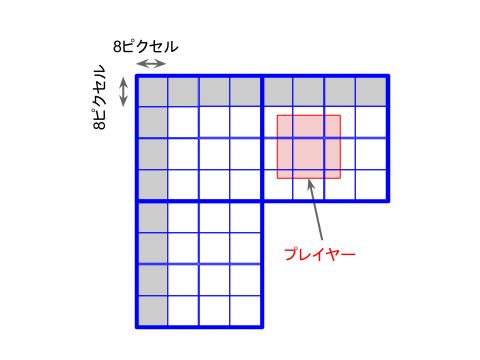
マップデータのイメージは下図のような感じです。
太線が迷路の1部屋、細線がマップの1マスです。
迷路の壁は1マス幅、通路は3マス幅になっています。
画面上では迷路の1部屋をBG4枚=32×32ピクセルで表示していますので、マップの1マスは8×8ピクセル相当になります。
このマップ自体はプログラムの内部で使うだけなので、キャラ番号などを気にする必要はなく、壁と通路が区別できれば十分です。
まずは、このマップを作成するプログラムです。
(今回はプログラムが長いので、テキストは最後に掲載します)
マップにも配列変数を使います。配列のサイズは迷路のサイズ(M_W、M_H)の4倍に右端の1列と最下行の1行を追加したものになります。
配列の各要素には、壁がある場所には1を代入します。壁が無い場所は初期値(0)です。
横に4つ、または縦に4つ、値を代入する必要があるので、行数だけは多いですが、ループを回して、迷路の各部屋を表す配列R[]を参照しながら、マップの配列MAP[]に代入するだけの、簡単な処理です。
なお、部屋の状態をチェックするのに、==ではなくANDを使っています。状態3のときは状態1の処理と状態2の処理を両方行いたいのでこのようにしています。
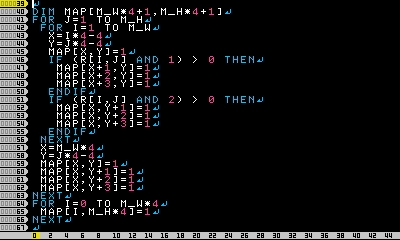
配列の処理完了後のイメージは下の図のようになります。これは5×5の迷路です。
マップは1マスを1つの数字でプリントしています。
右側の迷路に対応する配列の値は、左側のようになります。
壁が1、通路が0になっていますね。
次に、プレイヤーのキャラクタが、指定された場所へ移動できるかどうかを、このマップを使って判定します。
ただ、マップは8×8ピクセル単位ですが、キャラクタは1ピクセル単位でスムーズに動かしたいですね。
そのための処理はちょっと複雑です。
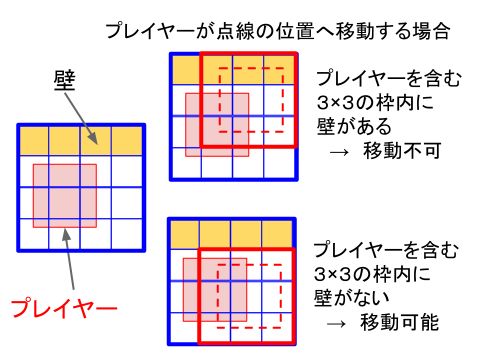
下の図の左の絵を見てください。
プレイヤーのキャラクタのサイズは16×16ピクセルですので、大きさとしてはマップの2×2マス相当です。
しかし、キャラクターはピクセル単位で移動しますので、実際には3×3マスの範囲にまたがって存在しています。
ここで、プレイヤーが図の右の絵の点線の位置へ移動しようとしているとします。
右上の絵では、キャラクタが壁にぶつかっていますので、この位置に移動することはできません。
右下はキャラクタが通路の中へ移動していますので、この位置へは移動可能です。
この絵をよく見ると、指定された位置へ無条件に移動して良いかどうかの判定は、プレイヤーのキャラクタを含む3×3マスの中に、壁が含まれているかどうかで判定できることが分かります。
では、3×3マスの中に壁が含まれていた場合は、「プレイヤーは動けない」のでしょうか?
確かに、指定された位置へ移動したらキャラクタが壁の中にめり込んでしまいます。
しかし実際には、プレイヤーは進みたい位置ではなく、「進みたい方向」を指示しているのだと考えられます。
であれば、可能な範囲でキャラクタを動かしてあげたほうが良いでしょう。
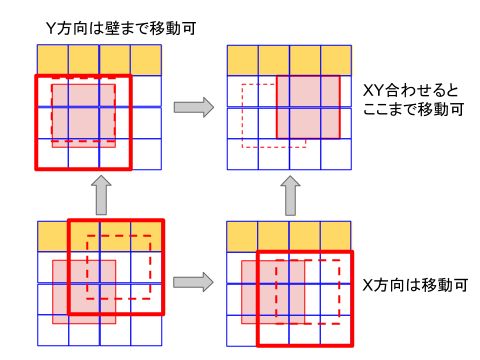
下の図を見てください。
左下の絵が、先ほどの「移動することができない状態」の絵です。
しかし、よく見ると、移動の横方向の成分だけを取り出せば(図右下)、移動することはできます。
また、縦方向の成分についても、壁の手前までは移動することができます(図左上)。
つまり、「指定した位置には移動することができない」場合でも、実は図右上に示した位置までは移動することができるのです。
このような処理をしてやると、ゲームの操作性がかなり向上します。
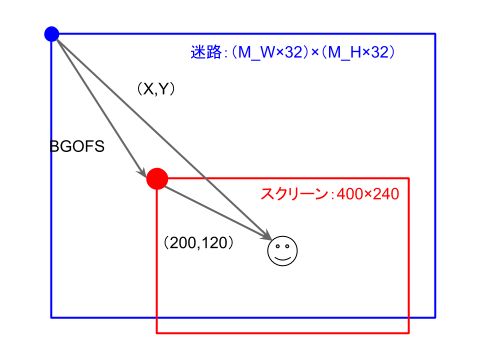
次に、キャラクタの位置に応じて迷路をスクロールする処理ですが、座標同士の関係を下の図で説明します。
迷路が描かれたBGは、1つの部屋あたり32×32ピクセルの1枚の大きな画像です。
そしてプレイヤーのキャラクタは、プレイヤーにとっては、この大きな画像の原点から見て座標(X,Y)に乗っています。
一方、表示としては、プレイヤーのキャラクタはスクリーンの中央に固定されています。
スクリーンのサイズは400ピクセル×240ピクセルですので、プレイヤーのキャラクタはスクリーンの原点から見て常に(200,120)の位置にあります。
そして、スクリーンの原点(赤丸)とBGの原点(青丸)の位置関係はBGOFS命令で指定します。
この関係を式で表すと、
BGOFS=(X,Y)-(200,120)
が常に成り立っています。
以上の処理をまとめた、プレイヤーのキャラクタ移動のプログラムは下図のようになります。
まず、88行目のDEF文を見てください。
ここでは、関数COUNT_WALLを定義しています。
この関数はマップの中の指定した3×3の領域の中に、壁がいくつあるかを数え、その数を返します。
関数のパラメータは、マップを表す配列と、3×3の領域の左上の座標です。
マップは壁のある場所が1、無い場所は0ですので、3×3の領域の中の壁の個数がN_Wに入り、その値が関数の呼び出し側に返されます。
ではプログラムの先頭から見ていきます。
SPSET 0,502
SPOFS 0,192,108,0
X=8:Y=8
@LOOP
最初の2行でスクリーンの中央に502番のキャラクタをスプライトで表示しています。
スプライトの基準点がスプライト自身の左上になるので、画面の中央にスプライトを置くための座標は(200,120)ではなくそこから8ピクセルだけ左上に移動した(192,112)にしています。
次のXとYは、プレイヤーのキャラクタのBG上での初期座標です。左端、上端は壁がありますので、(8,8)が迷路の左上隅の通路になります。
ループの中は、まずスライドパッドの値を読み取って、移動先の位置を(X_NEW,Y_NEW)に代入します。
今回は、パッドの読み取り値を3倍していますので、最大で一度に3ピクセルだけ縦横に移動します。
STICK OUT DX,DY
X_NEW=X+DX*3:Y_NEW=Y-DY*3
次に、COUNT_WALLを使って、移動先の壁の有無を調べます。
COUNT_WALLのパラメータは、マップを表す配列とマップ上での座標ですので、X_NEWとY_NEWはマップ上の座標に変換してから渡します。
この変換に使っている演算「>>3」は「3ビット右へシフト」ですが、ここでは「÷8」とほぼ同じと思ってください。
IF COUNT_WALL(MAP,X_NEW>>3,Y>>3)==0 THEN X=X_NEW ELSE X=MAX(MIN(X_NEW,X OR 7),X-(X AND 7)) ENDIF IF COUNT_WALL(MAP,X>>3,Y_NEW>>3)==0 THEN Y=Y_NEW ELSE Y=MAX(MIN(Y_NEW,Y OR 7),Y-(Y AND 7)) ENDIF
先に説明した「可能な範囲でキャラクタを動かしてあげる」処理をするため、X方向の移動処理とY方向の移動処理を別々に行っています。
そのため、COUNT_WALLを含む処理を2回連続で行っています。
1回目は「(可能な範囲で)X軸方向に移動」し、2回目は「(可能な範囲で)Y軸方向に移動」させています。
ここで「可能な範囲で」という部分ですが、「可能な範囲」とは、「マップ上での位置(マス)が変わらない範囲」つまり「8ピクセル単位のマス目を超えない範囲」です。
この計算をしているのが
X=MAX(MIN(X_NEW,X OR 7),X-(X AND 7))
という部分です。
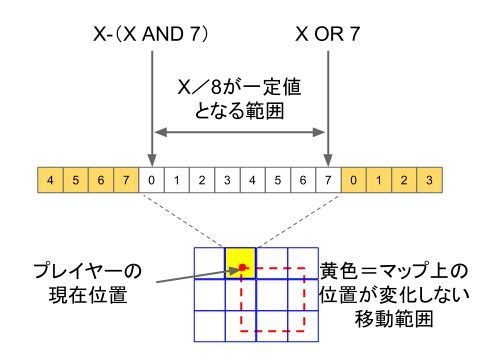
X OR 7とかX-(X AND 7)とか謎の式が並んでいるように見えるかもしれませんが、これらの値は下図の様な関係になっています。
Xがマップのあるマス目の中にあるとき、
・そのマス目の中にある一番小さいXの値: X-(X AND 7)
・そのマス目の中にある一番大きいXの値: X OR 7
です。
この範囲での位置移動なら、マップ上での位置は変化しないので、壁との衝突は起こりません。(現在すでにその場所にいるのですから!)
ある値X_NEWが与えられたとき、その値が必ず「X-(X AND 7)以上X OR 7以下」の範囲に入るように変更したいのですが、それには
X_NEW と X OR 7 の値のうち小さいほうを取り
その値と X-(X AND 7)の値のうち大きいほうをX_NEWとする
とすれば、X_NEWはX OR 7より大きくならず、またX-(X AND 7)より小さくならないことが保証できます。
上のプログラムは、この処理を1行で行っているだけです。
そして最後に、X,YをBGOFSのパラメータに変換して終了です。
この座標の変換については先ほど説明しました。
今回は以上ですが、ちょっと長かったですね・・・。
あらためて全部説明しようとすると、結構いろいろと解説しなければならないことがあるものですね。
最後に今回のプログラムのコード全体を掲載しておきます。
迷路のサイズは49×24だと広すぎる感じでしたので15×10にしています。
M_W=15:M_H=10 DIM R[M_W+2,M_H+2] FOR J=0 TO M_H+1 FOR I=0 TO M_W+1 IF I==0 || I==M_W+1 || J==0 || J==M_H+1 THEN R[I,J]=0 ELSE R[I,J]=3 ENDIF NEXT NEXT FOR J=1 TO M_H FOR I=1 TO M_W R_N=R[I,J-1] R_W=R[I-1,J] IF R_N==0 && R_W>0 THEN R[I,J]=1 IF R_N>0 && R_W==0 THEN R[I,J]=2 IF R_N>0 && R_W>0 THEN R[I,J]=1+RND(2) NEXT NEXT ACLS BGSCREEN 0,M_W*2+1,M_H*2+1 W1=292:W2=12580:W3=291:WE=257 FOR J=1 TO M_H FOR I=1 TO M_W IF R[I,J]==3 THEN C1=W3:C2=W1:C3=W2 IF R[I,J]==2 THEN C1=W2:C2=WE:C3=W2 IF R[I,J]==1 THEN C1=W1:C2=W1:C3=WE BGPUT 0,I*2-2,J*2-2,C1 BGPUT 0,I*2-1,J*2-2,C2 BGPUT 0,I*2-2,J*2-1,C3 BGPUT 0,I*2-1,J*2-1,WE NEXT BGPUT 0,M_W*2,(J-1)*2,W2 BGPUT 0,M_W*2,J*2-1,W2 NEXT BGFILL 0,0,M_H*2,M_W*2-1,M_H*2,292 BGPUT 0,M_W*2,M_H*2,256 DIM MAP[M_W*4+1,M_H*4+1] FOR J=1 TO M_H FOR I=1 TO M_W X=I*4-4 Y=J*4-4 MAP[X,Y]=1 IF (R[I,J] AND 1) > 0 THEN MAP[X+1,Y]=1 MAP[X+2,Y]=1 MAP[X+3,Y]=1 ENDIF IF (R[I,J] AND 2) > 0 THEN MAP[X,Y+1]=1 MAP[X,Y+2]=1 MAP[X,Y+3]=1 ENDIF NEXT X=M_W*4 Y=J*4-4 MAP[X,Y]=1 MAP[X,Y+1]=1 MAP[X,Y+2]=1 MAP[X,Y+3]=1 NEXT FOR I=0 TO M_W*4 MAP[I,M_H*4]=1 NEXT SPSET 0,502 SPOFS 0,192,112,0 X=8:Y=8 @LOOP STICK OUT DX,DY X_NEW=X+DX*3:Y_NEW=Y-DY*3 IF COUNT_WALL(MAP,X_NEW>>3,Y>>3)==0 THEN X=X_NEW ELSE X=MAX(MIN(X_NEW,X OR 7),X-(X AND 7)) ENDIF IF COUNT_WALL(MAP,X>>3,Y_NEW>>3)==0 THEN Y=Y_NEW ELSE Y=MAX(MIN(Y_NEW,Y OR 7),Y-(Y AND 7)) ENDIF BGOFS 0,X-192,Y-112,0 VSYNC 1 GOTO @LOOP DEF COUNT_WALL(MAP,PX,PY) N_W=0 FOR J=0 TO 2 FOR I=0 TO 2 N_W=N_W+MAP[PX+I,PY+J] NEXT NEXT RETURN N_W END




コメント